Cho 2 đường tròn (C) x2 +y2 -1=0 và (C'): x2 +y2 -2(m+1)x +4my -5=0. Tìm m để (C) và (C') tiếp xúc nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
CM
30 tháng 11 2019
Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
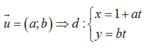
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
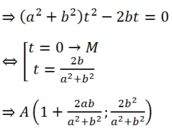
- Nếu d cắt (C2) tại B:
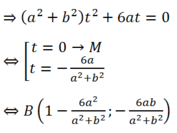
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
CM
20 tháng 10 2019
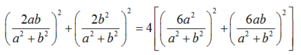
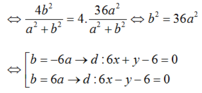
Đường tròn đã cho có tâm I − 3 2 ; 5 2
Bán kính đường tròn là: R = − 3 2 2 + 5 2 2 + 2 = 21 2
Độ dài I M = − 2 + 3 2 2 + 1 − 5 2 2 = 5 2 < R
Do đó, điểm M nằm trong đường tròn.
Qua M không kẻ được tiếp tuyến nào đến đường tròn.
ĐÁP ÁN A
CM
15 tháng 11 2019
Đường tròn (C): x 2 + y 2 + 4 x − 2 y − 4 = 0 có tâm I(-2; 1) và bán kính R = 3.
Ta có : I M = 1 + 2 2 + 2 − 1 2 = 10 > 3 nên M nằm ngoài đường tròn.
Qua M kẻ được hai tiếp tuyến đến đường tròn.
ĐÁP ÁN C
CM
3 tháng 9 2017
(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C
CM
4 tháng 7 2019
Đáp án: A
Ta có:
(C): x 2 + y 2 + 2x + 2y - 2 = 0 ⇔ (x + 1 ) 2 + (y + 1 ) 2 = 4 ⇒ I(-1;-1)
Phương trình tiếp tuyến của đường tròn tại M là đường thẳng đi qua M và nhận vector IM = (0;2) làm vecto pháp tuyến: 0.(x + 1) + 2.(y - 1) = 0 ⇔ y - 1 = 0
CM
2 tháng 11 2017
Ta sẽ xét xem trong 3 điểm A, B, C điểm nào nằm trong, điểm nào nằm ngoài đường tròn. Từ đó ta sẽ biết được đường tròn cắt những cạnh nào của tam giác ABC.
Ta có: ( - 1 ) 2 + 2 2 + 3 . ( - 1 ) - 5 . 2 + 2 = - 6 < 0 nên điểm A nằm trong đường tròn
3 2 + 0 2 + 3 . 3 – 5 . 0 + 2 = 15 > 0 nên điểm B nằm ngoài đường tròn
Và 2 2 + 3 2 + 3 . 2 - 5 . 3 + 2 = 4 > 0 nên điểm C nằm ngoài đường tròn.
Do vậy đường tròn cắt hai cạnh của tam giác là AB và AC.
Chọn C.
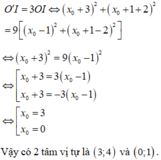
Đường tròn (C) tâm \(A\left(0;0\right)\) bán kính \(R=1\)
Đường tròn \(\left(C'\right)\) tâm \(B\left(m+1;-2m\right)\) bán kính \(r=\sqrt{5m^2+2m+6}\)
TH1: 2 đường tròn tiếp xúc ngoài
\(\Leftrightarrow AB=R+r'\)
\(\Rightarrow\sqrt{5m^2+2m+1}=1+\sqrt{5m^2+2m+6}\)
Đặt \(\sqrt{5m^2+2m+1}=t>0\)
\(\Rightarrow t=1+\sqrt{t^2+5}\)
\(\Leftrightarrow\sqrt{t^2+5}=t-1\left(t\ge1\right)\)
\(\Leftrightarrow t^2+5=t^2-2t+1\)
\(\Rightarrow t=-2\left(l\right)\)
TH2: 2 đường tròn tiếp xúc trong
\(\Rightarrow AB=r-R\)
\(\Leftrightarrow\sqrt{5m^2+2m+1}=\sqrt{5m^2+2m+6}-1\)
Đặt \(\sqrt{5m^2+2m+1}=t>0\)
\(\Rightarrow t=\sqrt{t^2+5}-1\)
\(\Leftrightarrow t+1=\sqrt{t^2+5}\)
\(\Leftrightarrow t^2+2t+1=t^2+5\Rightarrow t=2\)
\(\Rightarrow\sqrt{5m^2+2m+1}=2\)
\(\Leftrightarrow5m^2+2m-3=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=\frac{3}{5}\end{matrix}\right.\)