Câu 1: lập pt chính tắc của (E) biết (E) đi qua M (3/căn 5; 4/căn 5) và tam giác MF1F2 vuông tại M?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 11 2019
Đáp án A
Phương trình chính tắc của elip có dạng:
Do Elip đi qua nên:
Lại có :
Như vậy ta có hệ điều kiện:
Giải hệ ta được:
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2020
\(2c=8\Rightarrow c=4\)
Gọi pt elip có dạng: \(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\Leftrightarrow\frac{x^2}{a^2}+\frac{y^2}{a^2-16}=1\)
Do elip qua M nên:
\(\frac{15}{a^2}+\frac{1}{a^2-16}=1\)
\(\Leftrightarrow15\left(a^2-16\right)+a^2=a^2\left(a^2-16\right)\)
\(\Leftrightarrow a^4-32a^2+240=0\Rightarrow\left[{}\begin{matrix}a^2=20\\a^2=12< 16\left(l\right)\end{matrix}\right.\) \(\Rightarrow b^2=a^2-c^2=4\)
Phương trình (E): \(\frac{x^2}{20}+\frac{y^2}{4}=1\)
CM
1 tháng 12 2019
Gọi Elip cần tìm có dạng : (E) :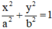 
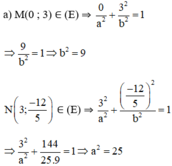
Vậy phương trình chính tắc của elip: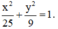 
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Elip có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\)
Do Elip đi qua điểm M(0;3) nên \(b = 3\)
Điểm \(N\left( {3; - \frac{{12}}{5}} \right)\) thuộc (E) nên ta có: \(\frac{{{3^2}}}{{{a^2}}} + \frac{{{{\left( { - \frac{{12}}{5}} \right)}^2}}}{{{3^2}}} = 1 \Leftrightarrow a = 5\)
Vậy Elip có phương trình chính tắc là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2020
Gọi pt (E) có dạng \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(e=\frac{c}{a}=\frac{2}{3}\Rightarrow c=\frac{2a}{3}\Rightarrow c^2=\frac{4a^2}{9}\)
\(\Rightarrow b^2=a^2-c^2=\frac{5a^2}{9}\)
Pt (E) có dạng: \(\frac{x^2}{a^2}+\frac{\frac{9}{5}y^2}{a^2}=1\Leftrightarrow a^2=x^2+\frac{9}{5}y^2\)
Thay tọa độ M vào ta được:
\(a^2=2^2+\frac{9}{5}\left(\frac{5}{2}\right)^2=\frac{61}{4}\Rightarrow b^2=\frac{305}{36}\)
Pt (E): \(\frac{x^2}{\frac{61}{4}}+\frac{y^2}{\frac{305}{36}}=1\)
13 tháng 4 2023
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1