X2-2(2m+1)x+3m2+6m
X-2
=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Δ=(4m+2)^2-4(3m^2+6m)
=16m^2+16m+4-12m^2-24m=4m^2-8m+4=(2m-2)^2
=>Phương trình luôn có 2 nghiệm
x1+2x2=16 và x1+x2=4m+2
=>x2=16-4m-2 và x1+2x2=16
=>x2=-4m+14 và x1=16+8m-28=8m-12
x1x2=3m^2+6m
=>-32m^2+48m+112m-168=3m^2+6m
=>m=12/5 hoặc m=2

Câu 1:
ĐKXĐ: x>=3
\(PT\Leftrightarrow\sqrt{x-3}=2x-m\)
=>x-3=(2x-m)^2
=>4x^2-4xm+m^2=x-3
=>4x^2-x(4m-1)+m^2+3=0
Δ=(4m-1)^2-4*4*(m^2+3)
=16m^2-8m+1-16m^2-48
=-8m-47
Để phương trình có nghiệm thì -8m-47>=0
=>m<=-47/8

Chọn B
Tập xác định của hàm số: ![]()
Ta có: ![]() .
.
![]()
![]()
![]()
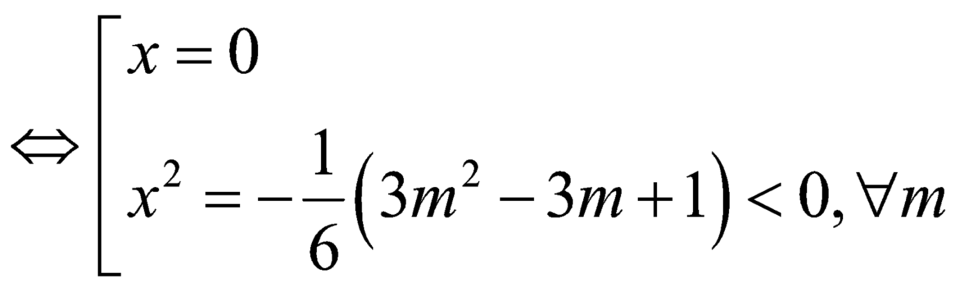
![]() .
.
Vì ![]() nên hàm số nghịch biến trên khoảng
nên hàm số nghịch biến trên khoảng ![]() .
.

Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì $\Delta'=(m+1)^2-4m\geq 0$
$\Leftrightarrow (m-1)^2\geq 0$
$\Leftrightarrow m\neq 1$
Khi đó, áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=4m$
Khi đó:
$(x_1+m)(x_2+m)=3m^2+12$
$\Leftrightarrow x_1x_2+m(x_1+x_2)+m^2=3m^2+12$
$\Leftrightarrow 4m+2m(m+1)+m^2=3m^2+12$
$\Leftrightarrow 3m^2+6m=3m^2+12$
$\Leftrightarrow 6m=12$
$\Leftrightarrow m=2$ (tm)

a)
Làm từng cái
(1)để có hai nghiệm: \(m^2+m+1\ne0\) ta có
\(m^2+m+1=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall m\)đúng với \(\forall m\)
(2) \(\Delta>0\Rightarrow\left(2m-3\right)^2-4\left(m-5\right)\left(m^2+m+1\right)>0\)
{để đó tý giải quyết sau }
(3) tích hai nghiệm phải dương
\(\Rightarrow x_1x_2=\dfrac{c}{a}>0\Rightarrow m-5>0\Rightarrow m>5\)
(4) tổng hai nghiệm phải dương
\(\Rightarrow-\dfrac{b}{a}>0\Rightarrow2m-3< 0\Rightarrow m< \dfrac{3}{2}\)
từ (3) (4) => không có m thỏa mãn => kết luận vô nghiệm
câu b)
có vẻ nhàn hơn
(1) \(\Delta'>0\Rightarrow9m^2-9m^2+2m-2=2m-2>0\Rightarrow m>1\)
(2)\(-\dfrac{b}{a}>0\Rightarrow m>0\)
(3) \(\dfrac{c}{a}>0\Rightarrow9m^2-2m+2>0\) đúng vơi mọi m
(1)(2)(3) nghiệm là: m>1