Tính diện tích hình chữ nhật ABCD dưới đây biết MA=MB và diện tích AMID=150 cm2 A B C D M I
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 5 2019
a) Chu vi hình chữ nhật ABCD là :
(45 + 15) ⨯ 2 = 120 (cm)
b) Chiều dài cạnh EB là :
EB = DC – AE = 45 – 15 = 30 (cm)
Diện tích hình thang EBCD là :
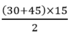= 562,5
(
c
m
2
)
c) Độ dài cạnh BM hoặc MC :
15 : 2 = 7,5 (cm)
Diện tích tam giác EBM là :
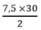= 112,5
(
c
m
2
)
Diện tích tam giác DMC = 168,75 ( c m 2 )
Tổng diện tích tam giác EBM và DMC là :
112,5 + 168,75 = 281,25 ( c m 2 )
Diện tích tam giác EDM là :
562,5 – 281,25 = 281,25 ( c m 2 )
Đáp số : a) 120cm ; b) 562,5 ( c m 2 )
c) 281,25 ( c m 2 )
+ Xét tam giác ABD và tam giác BCD có
\(S_{ABD}=\frac{ABxAD}{2}\) mà AB=CD và AD=BC nên
\(S_{ABD}=\frac{CDxBC}{2}=S_{BCD}=\frac{S_{ABCD}}{2}\)
Hai tam giác trên có chung đáy BD nên đường cao hạ từ A xuống BD = đường cao hạ từ C xuống BD
Nối A với I
Xét tam giác AIM và tam giác BIM, hai tam giác này có cạnh đáy AM=BM và chung đường cao hạ từ I xuống AB nên
\(S_{AIM}=S_{BIM}=s\)
Xét hai tam giác AID và tam giác CID hai tam giác này có chung đáy DI và đường cao hạ từ A xuống BD = đường cao hạ từ C xuống BD nên \(S_{AID}=S_{CID}\)
Ta có:
\(S_{AMID}=S_{AID}+S_{AIM}=S_{CID}+S_{BIM}=150cm^2\)
\(S_{ABCD}=2xS_{ABD}=2x\left(S_{AMID}+S_{BIM}\right)=2x\left(150+s\right)=300+2xs\)(1)
\(S_{ABCD}=S_{AMID}+S_{CID}+S_{BIM}+S_{BIC}=150+150+S_{BIC}=300+S_{BIC}\)(2)
Từ (1) và (2) => \(2xs=S_{BIC}=2xS_{BIM}\) (3)
Xét tam giác ABD và tam giác BCM có \(BM=\frac{AB}{2}\) và đường cao BC=AD nên \(S_{BCM}=\frac{S_{ABD}}{2}=\frac{S_{ABCD}}{4}\)
Mà \(S_{BCM}=S_{BCI}+S_{BIM}=3xS_{BIM}=\frac{S_{ABCD}}{4}\Rightarrow S_{BIM}=\frac{S_{ABCD}}{12}\)
\(\Rightarrow S_{BIC}=2xS_{BIM}=\frac{S_{ABCD}}{6}\)
\(S_{BCD}=S_{BIC}+S_{CID}=\frac{S_{ABCD}}{2}\Rightarrow S_{CID}=\frac{S_{ABCD}}{2}-S_{BIC}=\frac{S_{ABCD}}{2}-\frac{S_{ABCD}}{6}=\frac{S_{ABCD}}{3}\)
Ta đã c/m ở trên là \(S_{CID}+S_{BIM}=150\) nên \(S_{CID}+S_{BIM}=\frac{S_{ABCD}}{3}+\frac{S_{ABCD}}{12}=\frac{5xS_{ABCD}}{12}=150\Rightarrow S_{ABCD}=360cm^2\)