Giúp mình bài khoanh này
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
\(Q=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\dfrac{2}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}-1=Ư\left(2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=-2\\\sqrt{x}-1=-1\\\sqrt{x}-1=1\\\sqrt{x}-1=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=-1\left(vn\right)\\\sqrt{x}=0\\\sqrt{x}=2\\\sqrt{x}=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=9\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
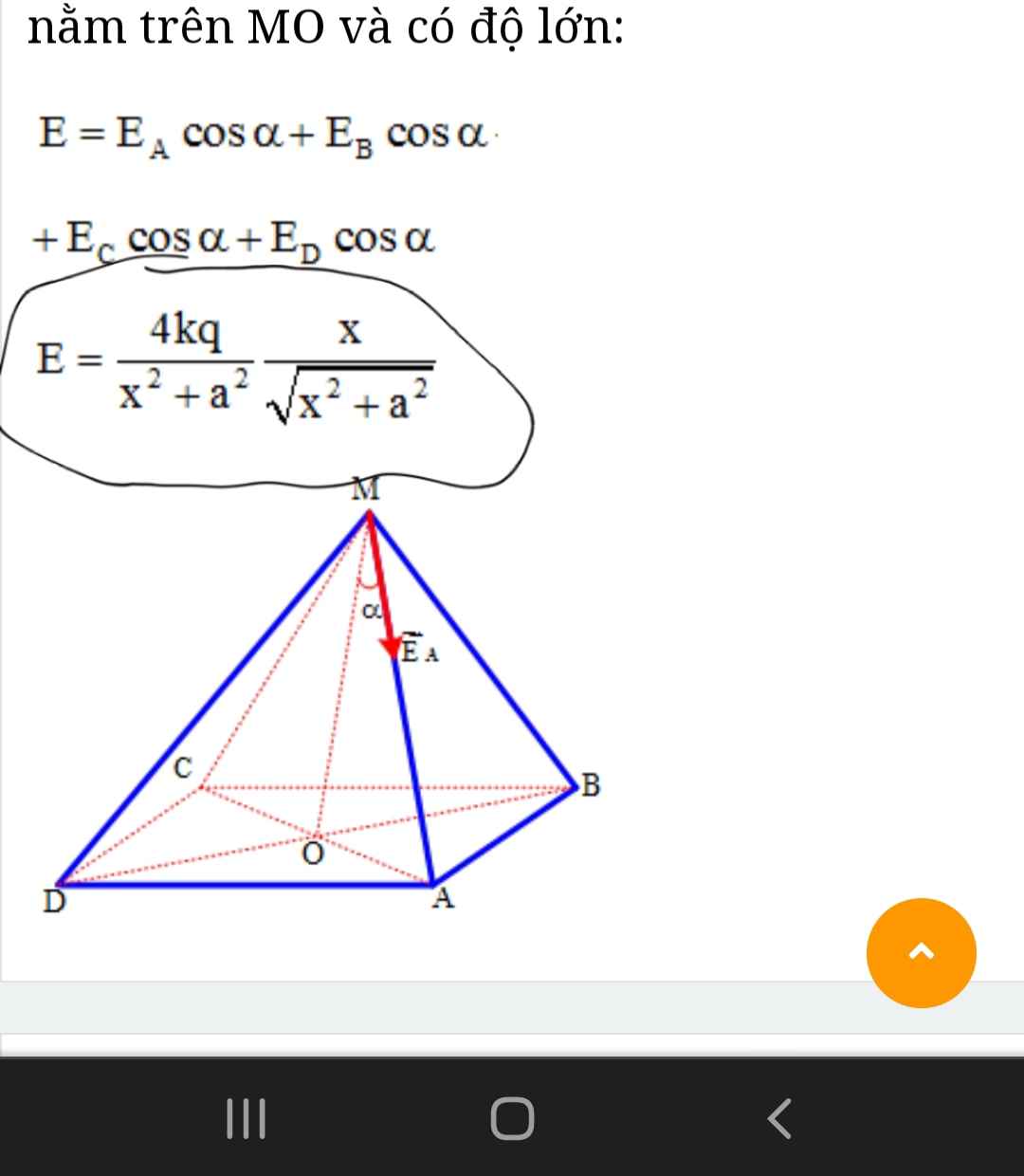
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)
2 tháng 7 2021
1 C => would
2 A => wish
3 A => hadn't said
4 A => hadn't sent
5 C => fluently
6 can => could
NN
2 tháng 7 2021
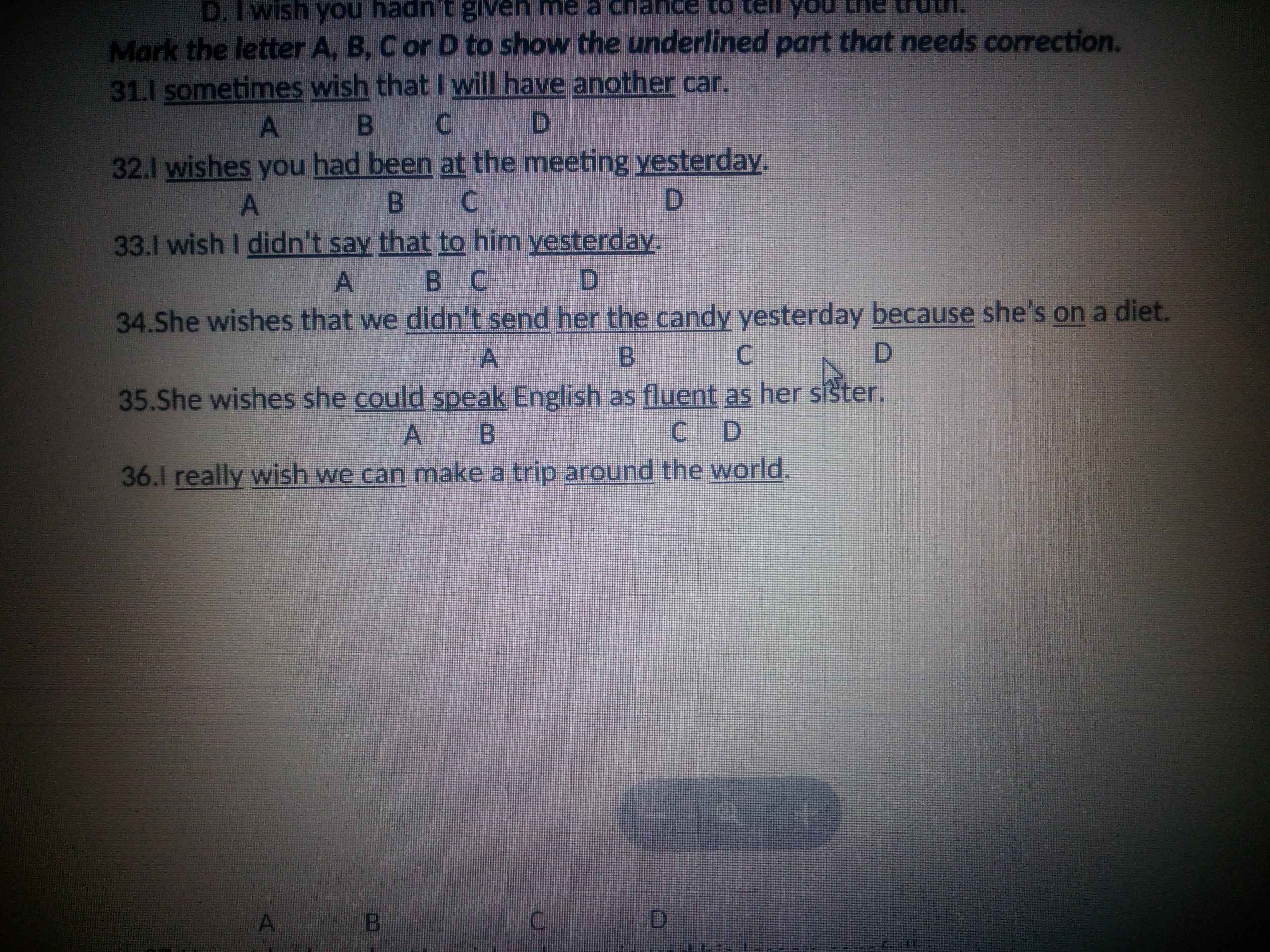
31d => would have
32a =>wish
33a => had not said
34 a => had not sent
35c => fluently
36can => could
NT
1
HA
1
30 tháng 3 2023
9:
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-2m+4\right)\)
=4m^2-4m^2+8m-16=8m-16
Để phương trình có hai nghiệm phân biệt thì 8m-16>0
=>m>2
x1^2+x2^2=x1+x2+8
=>(x1+x2)^2-2x1x2-(x1+x2)=8
=>(2m)^2-2(m^2-2m+4)-2m=8
=>4m^2-2m^2+4m-8-2m=8
=>2m^2+2m-16=0
=>m^2+m-8=0
mà m>2
nên \(m=\dfrac{-1+\sqrt{33}}{2}\)
BÀI KIỂM TRA LỚP 6 ĐÂY Á
Còn dài mấy đề nữa