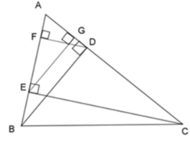
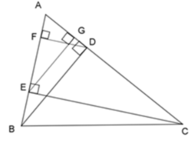
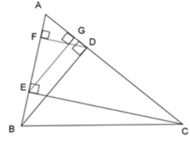
Cho ΔABC nhọn, các đường cao AA', BB', CC' cắt nhau tại H.
a) Tính Q = \(\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}\)
b) Gọi: AI là phân giác của góc BAC
IM là phân giác của góc AIC
IN là phân giác của góc AIB
Cm: AN.BI.CM = BN.IC.AM
c) \(Cm:\frac{\left(AB+BC+AC\right)^2}{AA'+BB'+CC'}\ge4\)