Chuyên ĐHSP HN ( năm 2014)
5) Cho hình vuông ABCD với tâm O. Gọi M là trung điểm cạnh AB. Các điểm N; P theo thứ tự thuộc cạnh BC; CD sao cho MN//AP.
Chứng minh rằng:
a) \(\Delta\)BNO ~ \(\Delta\)DOP và ^NOP = 45o
b) Tâm đường tròn ngoại tiếp \(\Delta\)NOP thuộc OC
c) Ba đường BD: AN; PM đồng quy

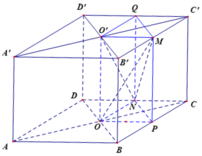

a) Gọi K là giao của MN và CD
Ta có: \(\widehat{BMN}=\widehat{MTD}\)(so le trong và MN//AP) và \(\widehat{MTD}=\widehat{APD}\) (đồng vị và MN//AP)
\(\Rightarrow\widehat{BMN}=\widehat{APD}\)
Xét \(\Delta BMN\)và \(\Delta DPA\)có:
\(\hept{\begin{cases}\widehat{MBN}=\widehat{PDA}\left(=90^o\right)\\\widehat{BMN}=\widehat{APD}\left(cmt\right)\end{cases}}\)
=> \(\Delta BMN~\Delta DPA\left(g.g\right)\Rightarrow\frac{BM}{DP}=\frac{BN}{DA}\Rightarrow\frac{BM}{BN}=\frac{DP}{DA}\)
Mà \(BM=\frac{AB}{2},DA=BD\sin\widehat{ABD}=\frac{\sqrt{2}BD}{2}=\sqrt{2}OB\)
Do đó: \(\frac{\frac{\sqrt{2}OD}{2}}{BN}=\frac{DP}{\sqrt{2}OB}\Rightarrow\frac{OD}{BN}=\frac{DP}{OB}\)
Xét \(\Delta DOP\)và \(\Delta BNO\)có: \(\hept{\begin{cases}\widehat{ODP}=\widehat{NBO}\left(=45^o\right)\\\frac{OD}{BN}=\frac{DP}{OB}\end{cases}\Rightarrow\Delta DOP~\Delta BNO\left(c.g.c\right)\Rightarrow\widehat{DOP}=\widehat{BNO}}\)
Mà \(\widehat{DON}=\widehat{BNO}+\widehat{OBN}=\widehat{BNO}+45^o\)
Và \(\widehat{DON}=\widehat{DOP}+\widehat{NOP}\)
Do vậy \(\widehat{NOP}=45^o\)
2. Ta có \(\frac{OP}{ON}=\frac{OD}{BN}\left(\Delta DOP~\Delta BNO\right)\)
Nên \(\frac{OP}{ON}=\frac{OB}{BN}\Rightarrow\frac{OP}{OB}=\frac{ON}{BN}\)
Xét \(\Delta OPN\)và \(\Delta BQN\)có: \(\hept{\begin{cases}\widehat{PON}=\widehat{OBN}\left(=45^o\right)\\\frac{OP}{OB}=\frac{ON}{BN}\end{cases}\Rightarrow\Delta OPN~\Delta BON\left(c.g.c\right)\Rightarrow\widehat{OPN}=\widehat{BON}}\)
Gọi I là tâm đường tròn ngoại tiếp tam giác NOP
Ta có \(\widehat{ION}=\frac{180^o-\widehat{OIN}}{2}=90^o-\widehat{OPN}=\widehat{BOC}-\widehat{BON}=\widehat{CON}\)
=> 2 tia OI,OC trùng nhau
Vậy I thuộc OC