Tìm a, b để đơn thức \(3ax^ay^bxy^2\)có hần hệ số là 9 và có bậc là 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sửa lại phần kết luận :
Vậy a=3 và b=3 thì đơn thức 3axaybxy2 c
ó phần hệ số là 9 và có bậc là 8
Để 3axaybxy2 có hệ số là 9 thì 3a=9
=>a=9:3=3
Ta có 3axaybxy2 =3axa+1yb+2
Để 3axa+1yb+2 có bậc là 9 thì (a+1)+(b+2)=9
Thay a=3 vào ta có:
(a+1)+(b+2)=9
Hay: (3+1)+(b+2)=9
=>4+(b+2)=9
=>b+2=5
=>b=3
3axayVậy a=3 và b=3 thì đơn thức 3axaybxy23axaybxy2 có phần hệ số là 9 và có bậc là 8

Thu gọn
-3axaybxy2 = -3axa + 1 yb + 2 1 điểm
Vì đơn thức có bậc là 7 và phần hệ số bằng -6 nên
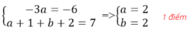

a) Ta có: \(A=\dfrac{3}{5}xy\cdot\left(-\dfrac{2}{5}xy^2z\right)\)
\(=\left(\dfrac{-3}{5}\cdot\dfrac{2}{5}\right)\cdot\left(x\cdot x\right)\cdot\left(y\cdot y^2\right)\cdot z\)
\(=\dfrac{-6}{25}x^2y^3z\)

Bài 7
\(-3y\left(x^2y^2\right)\left(-x^3y^9\right)=3x^5y^{12}\)
hệ sô : 3 ; biến x^5y^12 ; bậc 17

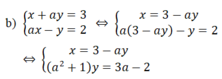
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
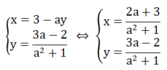
Khi đó:
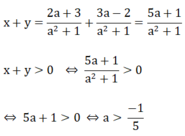
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0

c) Hệ phương trình đã cho có nghiệm
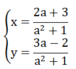
Theo đề bài : x= y
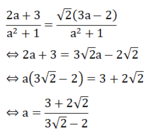
Vậy với 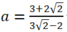 thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y
thì hệ phương trình có nghiệm (x; y) thỏa mãn x =
2
y