x^2+12x+35=0 hãy tính
a) x^1+x^2
b) x1^3+x2^3
c) (x1-x2)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 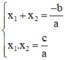
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 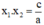
(Các bạn có thể làm cách 2 sử dụng điều kiện 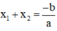 ).
).
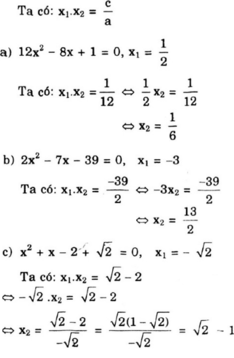
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0

Ta có: \(\hept{\begin{cases}x_1-x_2=5\\x_1^3-x_2^3=35\end{cases}}\)
<=> \(\hept{\begin{cases}x_1-x_2=5\\\left(x_1-x_2\right)^3+3x_1x_2\left(x_1-x_2\right)=35\end{cases}}\)
<=> \(\hept{\begin{cases}x_1-x_2=5\\5^3+3x_1x_2.5=35\end{cases}}\)
<=> \(\hept{\begin{cases}x_1-x_2=5\\x_1x_2=-6\end{cases}}\)
<=> \(\hept{\begin{cases}x_1=5+x_2\\\left(5+x_2\right)x_2=-6\end{cases}}\)
<=> \(\hept{\begin{cases}x_1=5+x_2\\x_2^2+5x_2+6=0\end{cases}}\)
<=> \(\hept{\begin{cases}x_1=5+x_2\\\left(x_2+3\right)\left(x_2+2\right)=0\end{cases}}\)
<=> \(\hept{\begin{cases}x_1=5+x_2\\x_2+3=0\end{cases}}\) hoặc \(\hept{\begin{cases}x_1=5+x_2\\x_2+2=0\end{cases}}\)
<=> \(\hept{\begin{cases}x_1=5-3=2\\x_2=-3\end{cases}}\) hoặc \(\hept{\begin{cases}x_1=5-2=3\\x_2=-2\end{cases}}\)
<=> \(\hept{\begin{cases}x_1+x_2=2-3=-1\\x_1x_2=-6\end{cases}}\) hoặc \(\hept{\begin{cases}x_1+x_2=3-2=1\\x_1x_2=-6\end{cases}}\)
Nếu x1, x2 là nghiệm của pt tm \(\hept{\begin{cases}x_1+x_2=-1\\x_1x_2=-6\end{cases}}\)là nghiệm của pt x2 + x - 6 = 0 = > a = 1; b = -6
Nếu x1, x2 là nghiệm của pt tm \(\hept{\begin{cases}x_1+x_2=1\\x_1x_2=-6\end{cases}}\) là nghiệm của pt x2 - x - 6 = 0 => a = -1 , b = -6
\(x_1^3-x_2^3=\left(x_1-x_2\right)^3+3x_1x_2\left(x_1-x_2\right)\)
\(\Leftrightarrow35=5^3+3x_1x_2.5\Leftrightarrow x_1x_2=-6\)
\(x_1-x_2=5\Leftrightarrow x_1=5+x_2\)
suy ra \(\left(5+x_2\right)x_2=-6\Leftrightarrow\orbr{\begin{cases}x_2=-2\Rightarrow x_1=3\\x_2=-3\Rightarrow x_1=2\end{cases}}\)
Với \(x_1=3,x_2=-2\Rightarrow x_1+x_2=1\)
thì \(x_1,x_2\)là hai nghiệm của phương trình: \(x^2-x-6=0\).
Với \(x_1=2,x_2=-3\Rightarrow x_1+x_2=-1\)
thì \(x_1,x_2\)là hai nghiệm của phương trình: \(x^2+x-6=0\).

a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25

Ta có: \(\Delta'=32>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=12\\x_1x_2=4\end{matrix}\right.\)
Mặt khác: \(T=\dfrac{x_1^2+x^2_2}{\sqrt{x_1}+\sqrt{x_2}}\)
\(\Rightarrow T^2=\dfrac{x_1^4+x^4_2+2x_1^2x_2^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(x_1^2+x_1^2\right)^2}{x_1+x_2+2\sqrt{x_1x_2}}\) \(=\dfrac{\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(12^2-2\cdot4\right)^2}{12+2\sqrt{4}}=1156\)
Mà ta thấy \(T>0\) \(\Rightarrow T=\sqrt{1156}=34\)

a) Ta có: \(x^2-11x-26=0\)
nên a=1; b=-11; c=-26
Áp dụng hệ thức Viet, ta được:
\(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-11\right)}{1}=11\)
và \(x_1x_2=\dfrac{c}{a}=\dfrac{-26}{1}=-26\)


Lời giải:
a) Khi $m=2$ thì pt trở thành:
$x^2-10x+15=0\Leftrightarrow (x-5)^2=10\Rightarrow x=5\pm \sqrt{10}$
b)
Để pt có 2 nghiệm pb $x_1,x_2$ thì trước tiên:
$\Delta'=(2m+1)^2-(4m^2-2m+3)>0$
$\Leftrightarrow 6m-2>0\Leftrightarrow m>\frac{1}{3}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2(2m+1)\\ x_1x_2=4m^2-2m+3\end{matrix}\right.\)
Để $(x_1-1)^2+(x_2-1)^2+2(x_1+x_2-x_1x_2)=18$
$\Leftrightarrow x_1^2+x_2^2-2(x_1+x_2)+2+2(x_1+x_2-x_1x_2)=18$
$\Leftrightarrow x_1^2+x_2^2-2x_1x_2=16$
$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=16$
$\Leftrightarrow 4(2m+1)^2-4(4m^2-2m+3)=16$
$\Leftrightarrow (2m+1)^2-(4m^2-2m+3)=4$
$\Leftrightarrow 6m-2=4\Leftrightarrow m=1$ (thỏa mãn)
vậy...........

a, Ta có : \(mx^3-x^2+2x-8m=0\)
\(\Leftrightarrow m\left(x^3-8\right)-\left(x^2-2x\right)=0\)
\(\Leftrightarrow m\left(x-2\right)\left(x^2+2x+4\right)-x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(mx^2+2mx+4m-x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(mx^2+x\left(2m-1\right)+4m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\mx^2+x\left(2m-1\right)+4m=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(TM\right)\\mx^2+x\left(2m-1\right)+4m=0\left(I\right)\end{matrix}\right.\)
- Để phương trình ban đầu có 3 nghiệm phân biệt lớn hơn 1
<=> Phương trình ( I ) có 2 nghiệm phân biệt lớn hơn 1 .
- Xét phương trình ( I ) có : \(\Delta=b^2-4ac=\left(2m-1\right)^2-4m.4m\)
\(=4m^2-4m+1-16m^2=-12m^2-4m+1\)
- Để phương trình ( I ) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow-\dfrac{1}{2}< m< \dfrac{1}{6}\) ( * )
- Theo vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1-2m}{m}\\x_1x_2=4\end{matrix}\right.\)
- Để phương trình ( I ) có nghiệm lớn hơn 1 \(\Leftrightarrow\left\{{}\begin{matrix}x_1-1+x_2-1>0\\\left(x_1-1\right)\left(x_2-1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1-4m}{m}>0\\5-\dfrac{1-2m}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1-4m}{m}>0\\\dfrac{7m-1}{m}>0\end{matrix}\right.\)
- Lập bảng xét dấu ( đoạn này làm tắt tí nha :vv )
Từ bảng xét dấu ta được : \(\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>\dfrac{1}{7}\end{matrix}\right.\\0< m< \dfrac{1}{4}\end{matrix}\right.\)
- Kết hợp điều kiện ( * ) ta được :\(\dfrac{1}{7}< m< \dfrac{1}{6}\)
Vậy ...
b, - Xét phương trình trên có : \(\Delta^,=b^{,2}-ac=\left(m-2\right)^2-\left(m-1\right)\left(m-3\right)\)
\(=m^2-4m+4-m^2+m+3m-3=1>0\)
Nên phương trình có 2 nghiệm phân biệt .
Theo vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2\right)}{m-1}\\x_1x_2=\dfrac{m-3}{m-1}\end{matrix}\right.\)
- Để \(x_1+x_2+x_1x_2< 1\)
\(\Leftrightarrow\dfrac{2\left(m-2\right)+\left(m-3\right)-\left(m-1\right)}{m-1}< 0\)
\(\Leftrightarrow\dfrac{2m-6}{m-1}< 0\)
- Đặt \(\dfrac{2m-6}{m-1}=f\left(m\right)\)
Cho f(m) = 0 => m = 3
m-1 = 0 => m = 1
- Lập bảng xét dầu :
m.............................1..........................................3...................................
2m-6............-..........|......................-.....................0...................+.................
m-1..............-............0...................+.....................|....................+.................
f(m).............+...........||..................-........................0................+....................
- Từ bảng xét dầu ta được : Để \(f\left(m\right)< 0\)
\(\Leftrightarrow1< m< 3\)
Vậy ...

1.
\(\Leftrightarrow6x^2-12x+7-6\sqrt{6x^2-12x+7}-7=0\)
Đặt \(\sqrt{6x^2-12x+7}=t>0\)
\(\Rightarrow t^2-6t-7=0\Rightarrow\left[{}\begin{matrix}t=-1\left(loại\right)\\t=7\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{6x^2-12x+7}=7\)
\(\Leftrightarrow6x^2-12x+7=49\Rightarrow x=1\pm2\sqrt{2}\)
2.
\(\Delta'=\left(m+1\right)^2-m^2-3=2m-2>0\Rightarrow m>1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+3\end{matrix}\right.\)
\(\left(x_1+x_2\right)^2-2x_1x_2=2x_1x_2+8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-8=0\)
\(\Leftrightarrow4\left(m+1\right)^2-4\left(m^2+3\right)-8=0\)
\(\Leftrightarrow2m-4=0\Rightarrow m=2\)