giải phương trình sau: 3(x+10)(2-x)=11 √(x2+8x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2022
\(\dfrac{2x-3}{2}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow\dfrac{3\left(2x-3\right)}{6}>\dfrac{8x-11}{6}\)
\(\Leftrightarrow3\left(2x-3\right)>8x-11\)
\(\Leftrightarrow6x-9>8x-11\)
\(\Leftrightarrow-2x>-2\)
\(\Leftrightarrow x< 1\)
Vậy \(S=\left\{x|x< 1\right\}\)
9 tháng 4 2022
\(2x-3\le8x-11\)
\(\Leftrightarrow-6x\le-8\)
\(\Leftrightarrow x\ge\dfrac{8}{6}\)
Vậy \(S=\left\{x|x\ge\dfrac{8}{6}\right\}\)
16 tháng 8 2021
a: Ta có: \(8x+11-3=5x+x-3\)
\(\Leftrightarrow8x+8=6x-3\)
\(\Leftrightarrow2x=-11\)
hay \(x=-\dfrac{11}{2}\)
b: Ta có: \(2x\left(x+2\right)^2-8x^2=2\left(x-2\right)\left(x^2+2x+4\right)\)
\(\Leftrightarrow2x\left(x^3+6x^2+12x+8\right)-8x^2=2\left(x^3-8\right)\)
\(\Leftrightarrow2x^4+12x^3+24x^2+16x-8x^2-2x^3+16=0\)
\(\Leftrightarrow2x^4+10x^3+16x^2+16x+16=0\)
\(\Leftrightarrow2x^4+4x^3+6x^3+12x^2+4x^2+8x+8x+16=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x^3+6x^2+4x+8\right)=0\)
\(\Leftrightarrow x+2=0\)
hay x=-2
16 tháng 8 2021
c: Ta có: \(\left(x+1\right)\left(2x-3\right)=\left(2x-1\right)\left(x+5\right)\)
\(\Leftrightarrow2x^2-3x+2x-3-2x^2-10x+x+5=0\)
\(\Leftrightarrow-10x+2=0\)
\(\Leftrightarrow-10x=-2\)
hay \(x=\dfrac{1}{5}\)
d: Ta có: \(\dfrac{1}{10}-2\cdot\left(\dfrac{1}{2}t-\dfrac{1}{10}\right)=2\left(t-\dfrac{5}{2}\right)-\dfrac{7}{10}\)
\(\Leftrightarrow\dfrac{1}{10}-t+\dfrac{1}{5}=2t-5-\dfrac{7}{10}\)
\(\Leftrightarrow-t-2t=-\dfrac{57}{10}-\dfrac{3}{10}=-6\)
hay t=2
CM
15 tháng 11 2018
a ) x 2 – 5 = 0 ⇔ x 2 = 5 ⇔ x 1 = √ 5 ; x 2 = - √ 5
Vậy phương trình có hai nghiệm x 1 = √ 5 ; x 2 = - √ 5
Cách khác:
x 2 – 5 = 0 ⇔ x 2 – ( √ 5 ) 2 = 0
⇔ (x - √5)(x + √5) = 0
hoặc x - √5 = 0 ⇔ x = √5
hoặc x + √5 = 0 ⇔ x = -√5
b)
x 2 – 2 √ 11 x + 11 = 0 ⇔ x 2 – 2 √ 11 x + ( √ 11 ) 2 = 0 ⇔ ( x - √ 11 ) 2 = 0
⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11
CM
2 tháng 4 2019
x2 – 2√11 x + 11 = 0
⇔ x2 – 2√11 x + (√11)2 = 0
⇔ (x - √11)2 = 0
⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11
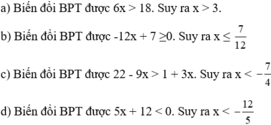
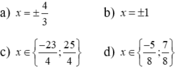
bớt đăng tùm bậy để kiếm điểm đi em ơi