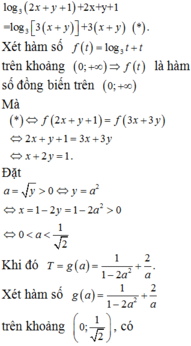Cho 22 số thực dương xx, yy thỏa mãn x≠1x≠1 và logxy=3logxy=3. Tính T=logx3y5T=logx3y5.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 6 2019
Đáp án C.
Ta có
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ log 3 x + y - log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ , có f ' t = 1 + 1 t ln 3 > 0 ; ∀ t > 0 .
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f[3(x + y)] = f(x2 + y2 + xy + 2)
CM
24 tháng 12 2018
Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.
CM
25 tháng 11 2019
Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
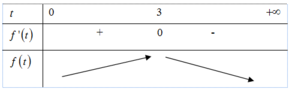
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
CM
15 tháng 9 2017
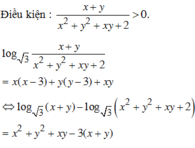
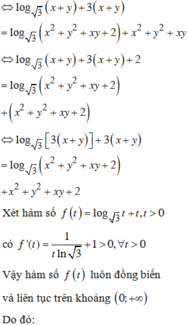
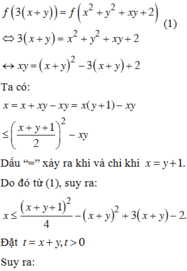
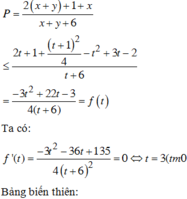
Đáp án D
Phương pháp giải:
Sử dụng phương pháp hàm đặc trưng để từ giả thiết suy ra mối liên hệ giữa hai biến, sau đó sử dụng phương pháp thể và khảo sát hàm số tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
TN
1 tháng 11 2016
Ta có: \(x+y=1\Rightarrow\left(x+y\right)^3=1\)
\(\Rightarrow x^3+y^3+3xy\left(x+y\right)=1\)
\(\Rightarrow x^3+y^3+3xy=1\)
\(\Rightarrow B=\frac{x^3+y^3+3xy}{x^3+y^3}+\frac{x^3+y^3+3xy}{xy}\)
\(=4+\frac{3xy}{x^3+y^3}+\frac{x^3+y^3}{xy}\)
Áp dụng Bđt Cô-si ta có:
\(\frac{3xy}{x^3+y^3}+\frac{x^3+y^3}{xy}\ge2\sqrt{\frac{3xy}{x^3+y^3}\cdot\frac{x^3+y^3}{xy}}=2\sqrt{3}\)
\(\Rightarrow B\ge4+2\sqrt{3}\)
Dấu = khi \(\hept{\begin{cases}x+y=1\\x^3+y^3=\sqrt{3xy}\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=1\\1-3xy=\sqrt{3xy}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y=1\\3\sqrt{xy}=\frac{-1+\sqrt{5}}{2}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x+y=1\\xy=\frac{6-2\sqrt{5}}{12}\end{cases}}\)
\(\Leftrightarrow x^2-x+\frac{6-2\sqrt{5}}{12}=0\)\(\Leftrightarrow x,y=\frac{1\pm\sqrt{\frac{2\sqrt{5}-3}{3}}}{2}\)
