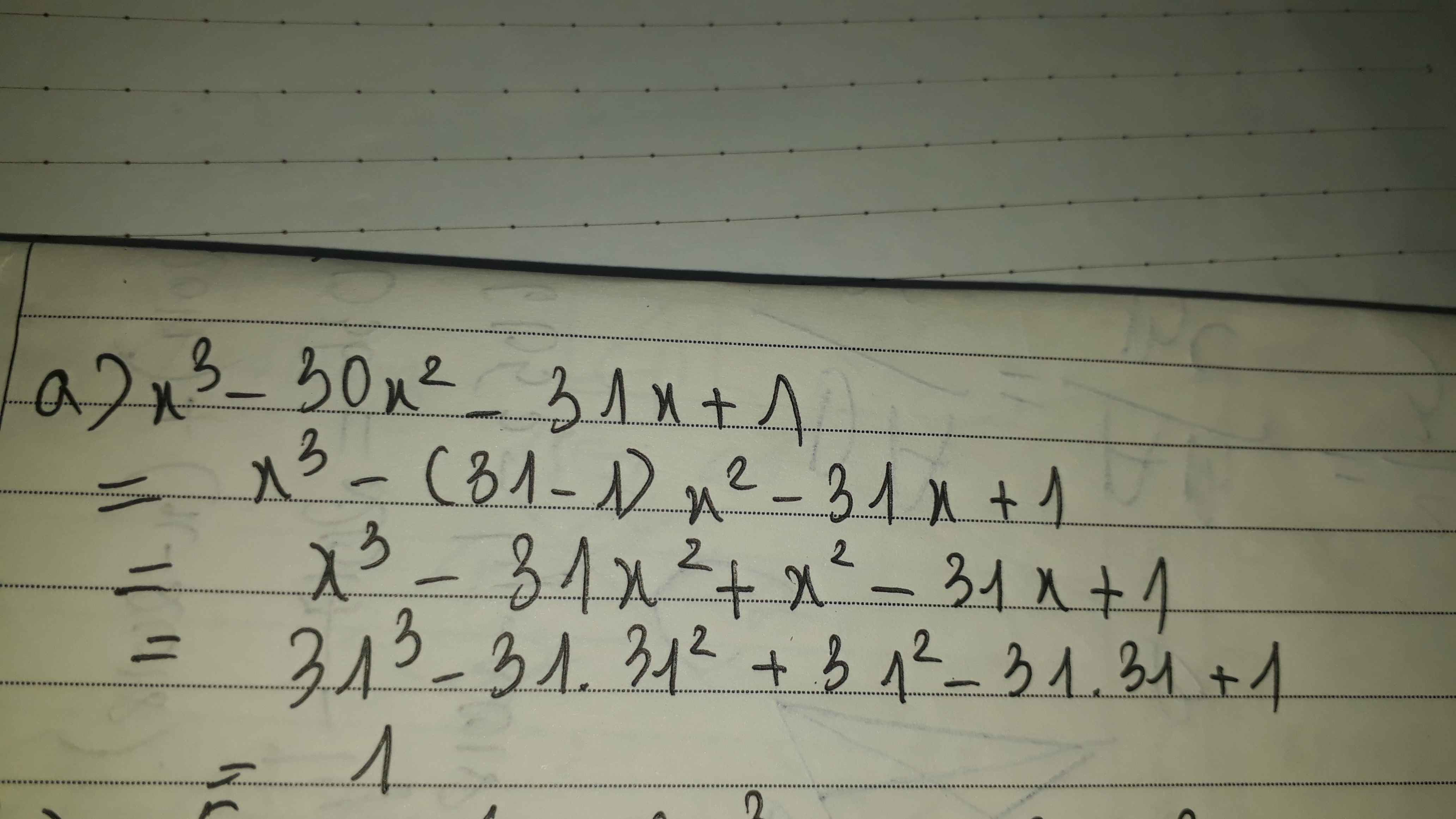\(\frac{120:30x2}{60x30:2}\)=.............
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 5 2016
30x2(2:3)+10=
=\(30x2+\frac{2}{3}+10\)
=\(60+\frac{2}{3}+10\)
=\(\frac{182}{3}+10\)
=\(\frac{212}{3}\)
23 tháng 1 2021
x4-30x2+31x-30 =0
<=> x4- x - 30x2+30x - 30 =0
<=> x ( x3- 1) - 30 (x2 - x + 1) =0
<=> x ( x-1) ( x2 - x + 1) - 30 (x2 - x + 1) =0
<=>(x ( x-1) - 30) ( x2 - x + 1) =0
<=>(x2 -x -30) ( x2 - x + 1) =0
<=>( x2 - x + 1) ( x2 - 5x + 6x - 30) =0
<=> ( x2 - x + 1) ( x(x-5) + 6 ( x-5)) =0
<=> ( x2 - x + 1) (x-5) (x+6) =0
Vì ( x2 - x + 1) > 0 với mọi x (bình phương thiếu)
=> (x-5) (x+6) =0
<=> x-5 = 0 hoặc x+ 6 = 0
<=> x=5 hoặc x = -6
NT
3
HN
22 tháng 1 2017
M(x) = x3 - 30x2 - 31x + 1
= (x3 - 31x2) + (x2 - 31x) + 1
= x2(x - 31) + x(x - 31) + 1
= 1
T1
các bạn giải hộ mình với :
a,X3 - 30X2 - 31X + 1 với X = 31
b,X5 - 15X4 + 16X3 - 29X2 + 13X với X = 14
4
CM
1 tháng 6 2019
a) Rút gọn P = x 4 y ; thay x = 10 và y = − 1 10 và biểu thức ta được P = 10 4 . − 1 10 = − 10 3 .
b) Nhận xét: Ta thấy biểu thức Q không thể rút gọn và việc thay trực tiếp x = 31 vào biểu thức khiến tính toán phức tạp. Với x = 31 thì 30 = 31 – 1 = x – 1.
Do đó Q = x 3 – ( x – 1 ) x 2 – x 2 + 1
Rút gọn Q = 1.
DP
6
AM
26 tháng 12 2016
2x8=16
3x9=27
4x5=15
5x6=30
20x4=80
30x3=90
12:2=6
12:3=4
2x9=18
5x7=35
90:3=30
40:2=20
18:3=6
30x2=90
27 tháng 2 2022
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;
7 tháng 7 2018
Với \(k\in N;k\ne0\) ta có :
\(\frac{1}{\left(k+1\right)\sqrt{k}+k\sqrt{\left(k+1\right)}}=\frac{1}{\sqrt{k\left(k+1\right)}\left(\sqrt{k}+\sqrt{k+1}\right)}\)
\(=\frac{\sqrt{k+1}+\sqrt{k}}{\sqrt{k\left(k+1\right)}\left(\sqrt{k+1}-\sqrt{k}\right)\left(\sqrt{k+1}+\sqrt{k}\right)}=\frac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}}\)
\(=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}\)
Áp dụng ta có :
\(M=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+....+\frac{1}{\sqrt{120}}-\frac{1}{\sqrt{121}}=1-\frac{1}{11}=\frac{10}{11}\)