rút gọn biểu thức √8+5√2 - √32 +6√1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 7 2019
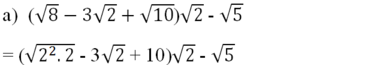
= (2√2 - 3√2 + 10)√2 - √5
= 2.(√2)2 - 3.(√2)2 + √10.√2 - √5
= 4 - 6 + √20 - √5 = -2 + 2√5 - √5
= -2 + √5
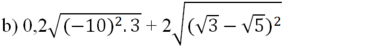
= 0,2.10.√3 + 2|√3 - √5|
s
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3 = 2√5
17 tháng 7 2023
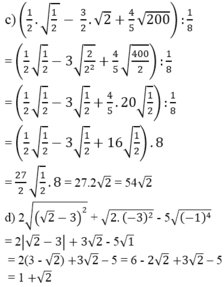
1) \(\sqrt{6+4\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{2^2+2\cdot2\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left|2+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=2+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}-1\)
2) \(\sqrt{21-4\sqrt{5}}+\sqrt{21+4\sqrt{5}}\)
\(=\sqrt{20-4\sqrt{5}+1}+\sqrt{20+4\sqrt{5}+1}\)
\(=\sqrt{\left(2\sqrt{5}\right)^2-2\sqrt{5}\cdot2\cdot1+1^2}+\sqrt{\left(2\sqrt{5}\right)^2+2\sqrt{5}\cdot2\cdot1-1^2}\)
\(=\sqrt{\left(2\sqrt{5}-1\right)^2}+\sqrt{\left(2\sqrt{5}+1\right)^2}\)
\(=\left|2\sqrt{5}-1\right|+\left|2\sqrt{5}+1\right|\)
\(=2\sqrt{5}-1+2\sqrt{5}+1\)
\(=4\sqrt{5}\)
PT
0
TN
1
DH
1
AH
Akai Haruma
Giáo viên
5 tháng 11 2023
Vì đây toàn là số cụ thể rồi nên không có đkxđ bạn nhé.
Lời giải:
a.
$=\sqrt{2}+4\sqrt{2}+6\sqrt{2}-3\sqrt{2}=8\sqrt{2}$
b.
$=\frac{13(5-2\sqrt{3})}{(5+2\sqrt{3})(5-2\sqrt{3})}+2\sqrt{3}=\frac{13(5-2\sqrt{3})}{13}+2\sqrt{3}$
$=5-2\sqrt{3}+2\sqrt{3}=5$
c.
$=2\sqrt{5}-|2-\sqrt{5}|=2\sqrt{5}-(\sqrt{5}-2)=\sqrt{5}+2$
HT
0
12 tháng 6 2023
\(\sqrt{9-3\sqrt{8}}-\dfrac{\sqrt{3}-1}{\sqrt{2}}+\sqrt{5-2\sqrt{6}}-\sqrt{2-\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{6}\right)^2-2.\sqrt{6}.\sqrt{3}+\left(\sqrt{3}\right)^2}-\dfrac{\sqrt{6}-\sqrt{2}}{2}+\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.\sqrt{2}+\left(\sqrt{2}\right)^2}-\dfrac{\sqrt{6}-\sqrt{2}}{2}\)
\(=\sqrt{\left(\sqrt{6}-\sqrt{3}\right)^2}-\sqrt{6}+\sqrt{2}+\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{6}-\sqrt{3}\right|-\sqrt{6}+\sqrt{2}+\left|\sqrt{3}-\sqrt{2}\right|\)
\(=\sqrt{6}-\sqrt{3}-\sqrt{6}+\sqrt{2}+\sqrt{3}-\sqrt{2}\) (do \(\sqrt{6}-\sqrt{3}>0;\sqrt{3}-\sqrt{2}>0\))
\(=0\)
12 tháng 6 2023
\(=\sqrt{9-6\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{2}}{2}+\sqrt{3}-\sqrt{2}-\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1\right)\)
\(=\sqrt{6}-\sqrt{3}-\dfrac{1}{2}\sqrt{6}+\dfrac{1}{2}\sqrt{2}+\sqrt{3}-\sqrt{2}-\dfrac{1}{2}\sqrt{6}+\dfrac{1}{2}\sqrt{2}\)
\(=0\)
\(\sqrt{8}+5\sqrt{2}-\sqrt{32}+6\sqrt{\frac{1}{2}}=2\sqrt{2}+5\sqrt{2}-4\sqrt{2}+3\sqrt{2}=\sqrt{2}\left(2+5-4+3\right)=6\sqrt{2}\)