Cho f(x)=x2 - 6x + 12. Giải PT: f(f(f(f(x))))=65539
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm

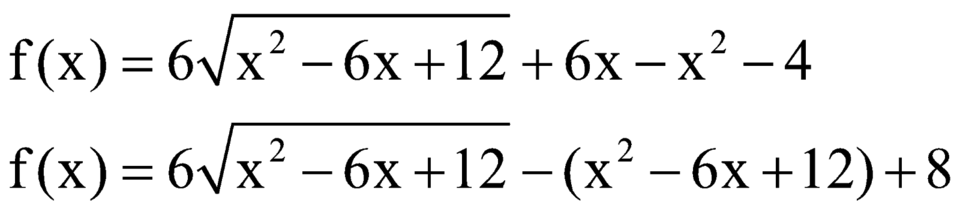
Đặt ![]()
khi đó ta có ![]()
Ta có ![]()
BBT:
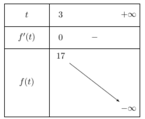
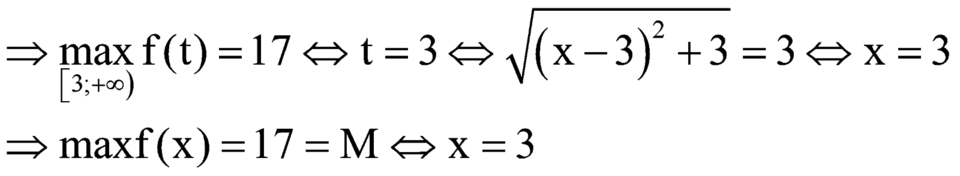
Vậy phương trình ![]() có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
Chọn B

\(a)\left(x-2\right)\left(x^2+2x-3\right)\ge0.\)
Đặt \(f\left(x\right)=\left(x-2\right)\left(x^2+2x-3\right).\)
Ta có: \(x-2=0.\Leftrightarrow x=2.\\ x^2+2x-3=0.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-3.\end{matrix}\right.\)
Bảng xét dấu:
x \(-\infty\) -3 1 2 \(+\infty\)
\(x-2\) - | - | - 0 +
\(x^2+2x-3\) + 0 - 0 + | +
\(f\left(x\right)\) - 0 + 0 - 0 +
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left[-3;1\right]\cup[2;+\infty).\)
\(b)\dfrac{x^2-9}{-x+5}< 0.\)
Đặt \(g\left(x\right)=\dfrac{x^2-9}{-x+5}.\)
Ta có: \(x^2-9=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-3.\end{matrix}\right.\)
\(-x+5=0.\Leftrightarrow x=5.\)
Bảng xét dấu:
x \(-\infty\) -3 3 5 \(+\infty\)
\(x^2-9\) + 0 - 0 + | +
\(-x+5\) + | + | + 0 -
\(g\left(x\right)\) + 0 - 0 + || -
Vậy \(g\left(x\right)< 0.\Leftrightarrow x\in\left(-3;3\right)\cup\left(5;+\infty\right).\)

Ta có f ' ( x ) = 3 x 2 + 2 x , g ' ( x ) = 2 x 2 + x + 2
f ' ( x ) < g ' ( x ) ⇔ 3 x 2 + 2 x < 2 x 2 + x + 2 ⇔ 3 x 2 + 2 x − 2 x 2 − x − 2 < 0 ⇔ x 2 + x − 2 < 0 ⇔ − 2 < x < 1
Vậy tập nghiệm bất phương trình là: S=(-2 ; 1).
Chọn đáp án B

1) - Thay x = 0 vào hàm số f(x) ta được :
\(f_{\left(0\right)}=-6.0+9=0\)
- Thay x = \(\frac{3}{2}\) vào hàm số f(x) ta được :
\(f_{\left(\frac{3}{2}\right)}=-6.\frac{3}{2}+9=0\)
2) - Thay \(f_{\left(x\right)}=-9\) vào hàm số trên ta được :
\(-6x+9=-9\)
=> \(-6x=-18\)
=> \(x=3\)
Vậy với f(x) = -9 thì x = 3 .
- Thay \(f_{\left(x\right)}=-x2\) vào hàm số trên ta được :
\(-6x+9=-x2\)
=> \(-4x=-9\)
=> \(x=\frac{9}{4}\)
Vậy với f(x) = -2x thì x = \(\frac{9}{4}\) .
1) f(0)= -6 . 0 +9 =9
f(3/2)=\(-6\cdot\frac{3}{2}+9=0\)
2) f(x)=-9 <=> -6x+9=-9 <=> -6x=-18 <=> x=3
\(f\left(x\right)=-x^2\\ \Leftrightarrow -6x+9=-x^2\\ \Leftrightarrow x^2-6x+9=0\\ \Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)