Chứng tỏ A = 3 1 + 3 2 + 3 3 + ⋯ + 3 60 chia hết cho 13
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=3^1+3^2+...+3^{60}\)
\(A=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\)
\(A=3\cdot\left(1+3+3^2\right)+3^4\cdot\left(1+3+3^2\right)+...+3^{58}\cdot\left(1+3+3^2\right)\)
\(A=3\cdot\left(1+3+9\right)+3^4\cdot\left(1+3+9\right)+...+3^{58}\cdot\left(1+3+9\right)\)
\(A=3\cdot13+3^4\cdot13+...+3^{58}\cdot13\)
\(A=13\cdot\left(3+3^4+...+3^{58}\right)\)
Mà: \(13\cdot\left(3+3^4+...+3^{58}\right)\) ⋮ 13
\(\Rightarrow A\) ⋮ 13


b: \(A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
\(a,\Leftrightarrow2A=8+2^3+2^4+...+2^{21}\\ \Leftrightarrow2A-A=8+2^3+2^4+...+2^{21}-4-2^2-2^3-...-2^{20}\\ \Leftrightarrow A=2^{21}+8-4-2^2=2^{21}\left(đpcm\right)\\ b,A=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+3^4+...+3^{58}\right)\\ A=13\left(3+3^4+...+3^{58}\right)⋮13\)

Số số hạng của B:
60 - 1 + 1 = 60 (số)
Do 60 chia hết cho 3 nên ta nhóm các số hạng của B thành nhóm 3 số hạng như sau:
B = 3 + 3² + 3³ + ... + 3⁶⁰
= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3⁵⁸ + 3⁵⁹ + 3⁶⁰)
= 3.(1 + 3 + 3²) + 3⁴.(1 + 3 + 3²) + ... + 3⁵⁸.(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3⁵⁸.13
= 13.(3 + 3⁴ + ... + 3⁵⁸) ⋮ 13
Vậy B ⋮ 13

Bạn tham khảo ở đây: Câu hỏi của Lê Diệu Chinh - Toán lớp 6 - Học toán với OnlineMath

A=3+3^2+3^3+....+3^60
A=(3+3^2+3^3+3^4)+(3^5+3^6+3^7+3^8)+....+(3^57+3^58+3^59+3^60)
A=39+3^4(3+3^2+3^3+3^4)+...+3^56.(3+3^2+3^3+3^4)
A=39+3^4.39+...+3^56.39
A=39.(1+3^4+...+3^56)\(⋮13\)
=>\(A⋮13\)

a) \(A=3^1+3^2+3^3+...+3^{60}\)
\(=\left(3^1+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\)
\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+3^4+...+3^{58}\right)⋮13\)
b) \(B=2+2^2+2^3+...+2^{20}\)
\(=\left(2+2^2+2^3+2^4\right)+...+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{17}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{17}\right)\div5\)
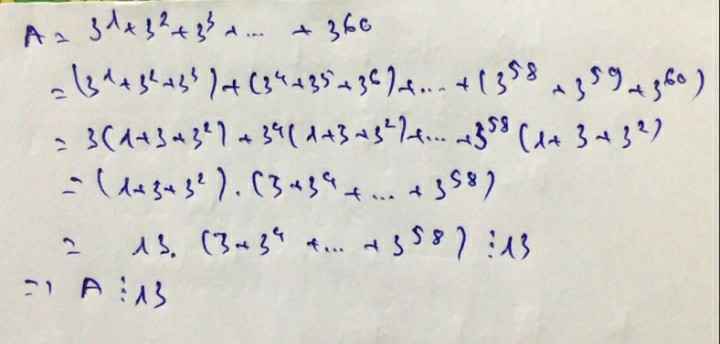
\(A=3^1+3^2+3^3+...+3^{60}\)
\(=\left(3^1+3^2+3^3\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\)
\(=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)