Cho 2 điểm M(−2;3;1),N(5;6;−2) có hình chiếu vuông góc lên trục Ox lần lượt là A,B khi đó tỷ số:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1 2022
Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M
Do A; B đối xứng qua M
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)
\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)
\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)
Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)
CM
14 tháng 2 2017
Chọn C.
Điểm M ∈ Ox ⇒ M(x; 0).
Khi đó 
ΔMAB vuông tại M nên 
Hay (–3 – x)(4 – x) + 2.3 = 0
⇔ –12 + 3x – 4x + x2 + 6 = 0
⇔ x2 – x – 6 = 0 ⇔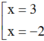 
.
Vậy: M1(3; 0), M2(-2; 0) và tổng hoành độ của chúng là : 3 + (-2) = 1.
30 tháng 11 2023
Bài 1:
\(y=\left(m-1\right)x^2+2mx-3m+1\)
\(=mx^2-x^2+2mx-3m+1\)
\(=m\left(x^2+2x-3\right)-x^2+1\)
Tọa độ điểm cố định mà (Pm) luôn đi qua là:
\(\left\{{}\begin{matrix}x^2+2x-3=0\\y=-x^2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=-x^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\y=-x^2+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3=0\\y=-x^2+1\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=0\\y=-x^2+1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-3\\y=-\left(-3\right)^2+1=-9+1=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-1^2+1=0\end{matrix}\right.\end{matrix}\right.\)
13 tháng 2 2022
a: Trên tia Oy, ta có: OM<OB
nên điểm M nằm giữa hai điểm O và B
=>BM+MO=BO
hay BM=3(cm)
Ta có: OM và OA là hai tia đối nhau
nên điểm O nằm giữa hai điểm A và M
=>OA+OM=AM
hay AM=3(cm)
Ta có: điểm M nằm giữa hai điểm A và B
mà MA=MB
nên M là trung điểm của AB
b: \(\widehat{tOy}=130^0\)
20 tháng 4 2023
a: Trên tia Oy, ta có: OM<OB
nên điểm M nằm giữa hai điểm O và B
=>BM+MO=BO
hay BM=3(cm)
Ta có: OM và OA là hai tia đối nhau
nên điểm O nằm giữa hai điểm A và M
=>OA+OM=AM
hay AM=3(cm)
Ta có: điểm M nằm giữa hai điểm A và B
mà MA=MB
nên M là trung điểm của AB
b: \(\widehat{tOy}\) = \(130^{o}\)
\(\Rightarrow A\left(-2;0;0\right)\Rightarrow OA=\left|x_A\right|=2\)
\(B\left(5;0;0\right)\Rightarrow OB=\left|x_B\right|=5\)
\(\frac{OA}{OB}=\frac{2}{5}\)
(Nếu \(\frac{\overrightarrow{OA}}{\overrightarrow{OB}}\) thì kết quả là \(-\frac{2}{5}\))
OA/OB=?