Cho tam giác ABC(AC>AB) đường phân giác AD.Trên cạnh AD lấy điểm E sao cho CDE=BAC.CMR DB=DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2022
a: Xét ΔCDE và ΔCAB có
\(\widehat{CDE}=\widehat{CAB}\)
\(\widehat{C}\) chung
Do đó: ΔCDE\(\sim\)ΔCAB
Câu b đề sai rồi bạn
4 tháng 4 2017
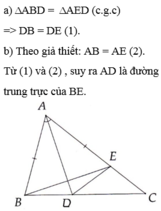
a) Xét tam giác ABD và tam giác AED có
AB=AE
BAD=DAE( vì AD là phân giác của BAC)
Cạnh AD chung
=> tam giác ABD= tam giác AED( c.g.c)
=>DB=DE
b) Có tam giác ABD= tam giác AED
=> ABD=AED
=>DBK=DEC( kề bù với 2 góc bằng nhau)
Xét tam giác BDK và tam giác EDC
BD=DE
BDK=EDC ( 2 góc đối đỉnh)
DBK=DEC
=> tam giác BDK= tam giác EDC ( g.c.g)
c) Tam giác BDK=tam giác EDC
=>DBK=DEC
Có DBK>C( DBK là góc ngoài tam giác ABC)
=>DEC>C
=>DC>DE
Mà DE=DE
=>DC>DB
24 tháng 12 2019
Mik sửa đề nha. vì đề bài cho mik k vẽ được.
" Cho tam giác ABC có AB<AC,AD là đường phân giác (D thuộc BC). trên cạnh AC lấy điểm E sao cho AB=AE. đường thẳng DE cắt đường thẳng AB tại K
CMR: a) DB = DE
b) AK = AC
c) GÓC DEC > GÓC ACB
A B C D E K
Làm
a) Xét tam giác ADB và tam giác ADE có:
AB = AE ( gt )
\(\widehat{BAD}=\widehat{EAD}\)( AD là tia phân giác góc A )
AD chung.
=> Tam giác ADB = tam giác ADE ( c.g.c )
=> BD = DE ( hai cạnh tương ứng )
b) Vì tam giác ADB = tam giác ADE ( cmt )
=> \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{DBK}=180^0\)( hai góc kề bù )
\(\widehat{AED}+\widehat{DEC}=180^0\)
Mà \(\widehat{ABD}=\widehat{AED}\)
=> \(\widehat{DBK}=\widehat{DEC}\)
Xét tam giác BDK và tam giác EDC có:
\(\widehat{DBK}=\widehat{DEC}\)( cmt )
BD = DE ( cmt )
\(\widehat{BDK}=\widehat{EDC}\)
=> Tam giác BDK = tam giác EDC ( g.c.g )
=> BK = EC
Ta có: AB + BK = AK
AE + EC = AC
=> Mà: AB = AE
BK = EC
=> AK = AC.
câu c kiểu j ý
# Học tốt#
