Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;0), B(3;4;1), D(−1;3;2). Tìm tọa độ điểm Csao cho ABCD là hình thang có hai cạnh đáy AB, CD và có góc C bằng...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;0), B(3;4;1), D(−1;3;2). Tìm tọa độ điểm Csao cho ABCD là hình thang có hai cạnh đáy AB, CD và có góc C bằng 45∘.
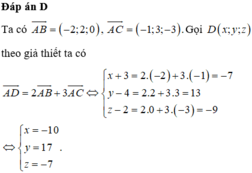
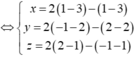
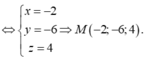
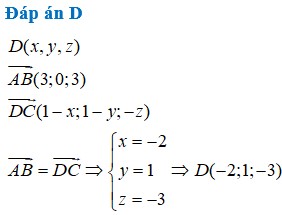
\(\overrightarrow{AB}=\left(2;2;1\right)\Rightarrow\) pt tham số của CD có dạng: \(\left\{{}\begin{matrix}x=-1+2t\\y=3+2t\\z=2+t\end{matrix}\right.\)
\(\Rightarrow C\left(-1+2t;3+2t;2+t\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CB}=\left(4-2t;1-2t;-1-t\right)\\\overrightarrow{CD}=t\left(-2;-2;-1\right)\end{matrix}\right.\)
\(cos45^0=\frac{\sqrt{2}}{2}=\frac{-2\left(4-2t\right)-2\left(1-2t\right)+1\left(1+t\right)}{\sqrt{4+4+1}.\sqrt{\left(4-2t\right)^2+\left(1-2t\right)^2+\left(1+t\right)^2}}\)
\(\Leftrightarrow\frac{t-1}{\sqrt{t^2-2t+2}}=\frac{\sqrt{2}}{2}\) (\(t>1\))
\(\Leftrightarrow2\left(t-1\right)^2=t^2-2t+2\)
\(\Leftrightarrow t^2-2t=0\Rightarrow\left[{}\begin{matrix}t=0\left(l\right)\\t=2\end{matrix}\right.\) \(\Rightarrow C\left(3;7;4\right)\)