Giải bất phương trình:
|-x2+3x+2|<_ x2-3x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
23 tháng 2 2022
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
CM
3 tháng 6 2019
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B
CM
6 tháng 4 2019
Chọn B
Bất phương trình có điều kiện xác định:
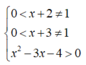
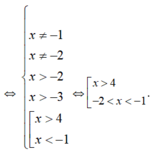
Vậy tập xác định của bất phương trình là 
- Với \(1< x< 2\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT vô nghiệm
- Với \(x\notin\left(1;2\right)\) hai vế ko âm, bình phương:
\(\left(-x^2+3x+2\right)^2\le\left(x^2-3x+2\right)^2\)
\(\Leftrightarrow\left(x^2-3x+2\right)^2-\left(-x^2+3x+2\right)^2\ge0\)
\(\Leftrightarrow4\left(2x^2-6x\right)\ge0\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge3\end{matrix}\right.\)
Kết hợp điều kiện ta được nghiệm của BPT là: \(\left[{}\begin{matrix}x\le0\\x\ge3\end{matrix}\right.\)