Phương trình mặt phẳng #Hỏi cộng đồng OLM #Toán lớp 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Do (P) → AB nên mp(P) có một vectơ pháp tuyến là
![]()
Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là
-2(x - 1) + (y - 0) + 4(z + 2) = 0 ⇔ 2x - y - 4z - 10 = 0

Đáp án A
Phương pháp: Cho u 1 → ; u 2 → là cặp vectơ chỉ phương của mặt phẳng (α), khi đó n → =[ u 1 → , u 2 → ] là một vectơ pháp tuyến của (α)
Cách giải:
Gọi mặt phẳng cần tìm là (α)
(P): x+3y
-
2z
-
1=0 có một VTPT ![]()
Vì ![]()
![]()
Khi đó, (α) có một vectơ pháp tuyến là: n → =[ u 1 → , u 2 → ] = (5; - 1;1)
Phương trình (α): 5x - y+z - 9=0

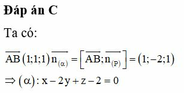

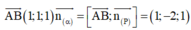

\(\overrightarrow{AB}=\left(2;-2;2\right)=2\left(1;-1;1\right)\)
Gọi I là trung điểm AB \(\Rightarrow I\left(1;0;2\right)\)
Phương trình (P) qua I và nhận \(\left(1;-1;1\right)\) là 1 vtpt:
\(1\left(x-1\right)-y+1\left(z-2\right)=0\)
\(\Leftrightarrow x-y+z-3=0\)