bài toán cổ ấn độ 1 cây bị gẫy cách gốc 1,5 mét. Tính chiều cao của cây (hình lớp 7)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE
hay ΔBAE cân tại B
b: Ta có: BA=BE
DA=DE
Do đó: BD là đườg trung trực của AE
hay BD\(\perp\)AE
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó:ΔADF=ΔEDC
Suy ra: DF=DC
mà DC>DE
nên DE<DF

Có bài gần giống bài của bn lè nhìn vào đó mà làm
Đây là đường lick của bài toán đó
https://olm.vn/hoi-dap/question/1185299.html
~Chucs bạn sớm giải được~

Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
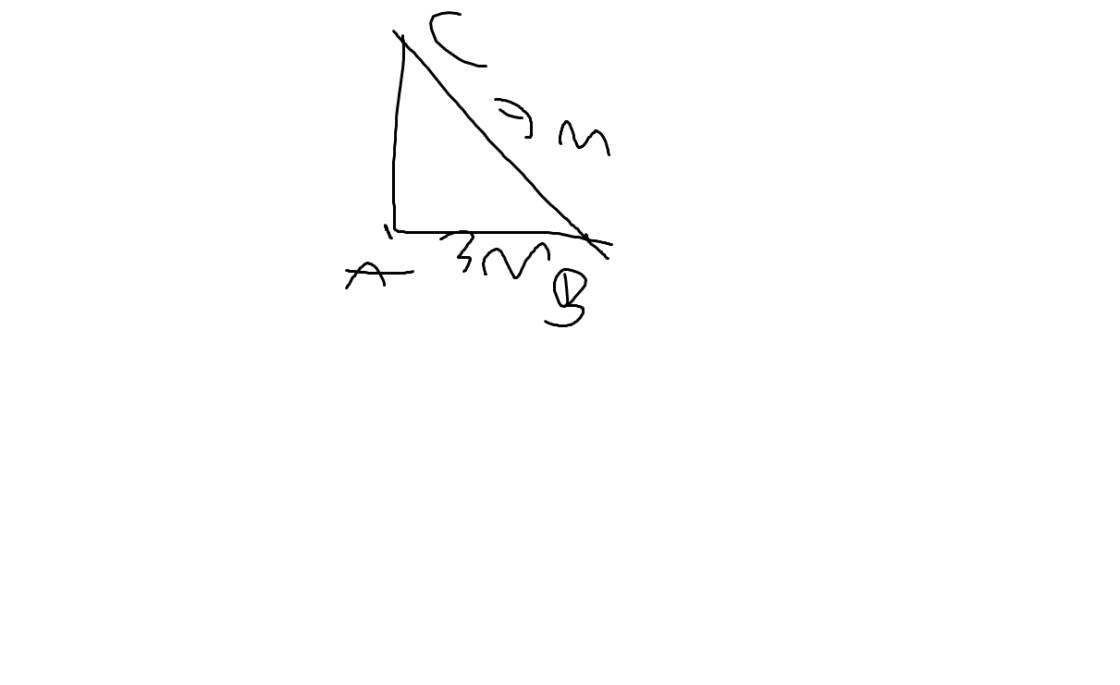
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)


Gọi gốc cây là A , điểm gãy là B , ngọn cây chạm đất là C ta được ΔABC
Theo đề bài , ta có : AB = 7m ; AC = 24m
Do cây luôn đứng vuông góc với mặt đất nên AB ⊥ AC
=> ΔABC vuông ở A
+) Áp dụng định lí Pi-ta-go trong ΔABC vuông tại A , ta có :
AB2+AC2=BC272+242=BC249+576=BC2625=BC2⇒BC=625−−−√=25(m)AB2+AC2=BC272+242=BC249+576=BC2625=BC2⇒BC=625=25(m)
+) Chiều dài khi cây chưa bị gãy là : AB + BC = 7 + 25 = 32 ( m )
Vậy cây cao 32m khi chưa bị gãy