TÌm tọa độ giao điểm của paradol(P): y = x2 và đường thẳng (d): y = 2x + 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
13 tháng 5 2021
Vì đường thẳng (d) cắt Oy tại điểm có tung độ bằng 8
Nên m+3=8⇔ m=5
Theo pt hoành độ giao điểm của (d) và (P)
Ta có:x2=2x+8x2=2x+8
⇔x2−2x−8=0x2−2x−8=0
Δ′=(−1)2−(−8)=9Δ′=(−1)2−(−8)=9
√Δ′=√9=3>0Δ′=9=3>0
Vậy pt có 2 nghiệm pb
x1=1+31=41+31=4
x2=1−31=−21−31=−2
Với x =4 thì y=x2=42=16
Với x =-2 thì y=x2=(-2)2=4
CM
5 tháng 2 2017
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình
1/2 x 2 = (-1)/2 x + 3 ⇔ x 2 + x - 6 = 0
Δ = 1 - 4.1.(-6) = 25 > 0
⇒ Phương trình có 2 nghiệm phân biệt
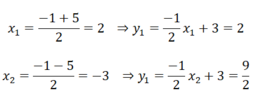
Vậy tọa độ giao điểm của (P) và (d) là (2; 2) và (-3; 9/2)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Phương trình hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)
a. Khi \(m=-1\), (1) trở thành:
\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)
b.
\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) cắt (P) tại 2 điểm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)
\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)
26 tháng 3 2022
Hoành độ giao điểm tm pt
\(x^2-3x+2=0\Leftrightarrow x=1;x=2\)
\(\Rightarrow y=1;y=4\)
Vậy (P) cắt (d) tại A(1;1) ; B(2;4)
CM
16 tháng 10 2018
Chọn đáp án A
Phương trình hoành độ giao điểm của (P) và (d) là:
x 2 = 2x - 1 ⇔ x 2 - 2x + 1 = 0 ⇔ x - 1 2 = 0 ⇔ x = 1
Với x = 1 ⇒ y = 1
⇒ Tọa độ giao điểm của (P) và (d) là (1; 1)
Phương trình hoành độ giao điểm giữa (P) và (d)
\(x^2=2x+3\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Delta=\left(-2\right)^2-4.1.\left(-3\right)=16>0\)
\(\Rightarrow x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-\sqrt{16}}{2.1}=-1\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{2+\sqrt{16}}{2.1}=3\)
Với x1 =-1 \(\Rightarrow\) y1 = (-1)2 =1 \(\Rightarrow\) A(-1;1)
x2 =3 \(\Rightarrow\)y2 =32 =9 \(\Rightarrow\)B(3;9)
Vậy tọa độ giao điểm là A(-1;1) và B(3;9)