Cho tam giác ABC cân tại A có A = 1200, hãy tính BC khi biết AB = c.
mik cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
2
AH
Akai Haruma
Giáo viên
7 tháng 10 2021
Lời giải:
Kẻ $AH\perp BC$. Vì $ABC$ cân tại $A$ nên đường cao $AH$ đồng thời là đường trung tuyến
$\Rightarrow H$ là trung điểm $BC$
$\Rightarrow BH=BC:2=2$ (cm)
Áp dụng định lý Pitago:
$AH=\sqrt{AB^2-BH^2}=\sqrt{6^2-2^2}=4\sqrt{2}$ (cm)
Diện tích $ABC$:
$S=\frac{AH.BC}{2}=\frac{4\sqrt{2}.4}{2}=8\sqrt{2}$ (cm vuông)
$\cos B = \frac{BH}{AB}=\frac{2}{6}=\frac{1}{3}$
$\Rightarrow \widehat{B}=70,5^0$
$\Rightarrow \widehat{C}=\widehat{B}=70,5^0$
$\widehat{A}=180^0-\widehat{B}-\widehat{C}=180^0-2. 70,5^0=39^0$
12 tháng 7 2023
a: Xét ΔAMB và ΔAMC có
AB=AC
góc BAM=góc CAM
AM chung
=>ΔAMB=ΔACM
b:
ΔABC cân tại A có AM là phân giác
nên AM vuông góc BC và M là trung điểm của BC
MB=MC=BC/2=3cm
=>AM =căn 5^2-3^2=4cm
c: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
góc B=góc C
=>ΔMHB=ΔMKC
=>MH=MK
Xét ΔHMQ vuông tại H và ΔKMP vuôg tại K có
MH=MK
góc HMQ=góc KMP
=>ΔHMQ=ΔKMP
=>MQ=MP
=>ΔMQP cân tại M
14 tháng 7 2023
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
11 tháng 1 2022
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
CM
13 tháng 8 2017
Đáp án A
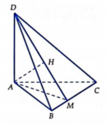
Trong mặt phẳng (ABC) Kẻ A M ⊥ B C
Trong mặt phẳng (SAM) kẻ A H ⊥ S M
⇒ d A ; S B C = A H
Ta có A M = A B . cos B A M ^ = A B . cos 60 0 = a 2
Diện tích tam giác ABC là S A B C = 1 2 A B . A C . sin 120 0 = 1 2 a 2 3 2 = a 2 3 4 Ta có
V S . A B C = 1 3 . S A . S A B C = 1 3 . S A . a 3 3 24 = a 3 3 24 ⇒ S A = a 2
Tam giác SAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 S A 2 + 1 A M 2 ⇒ A H = a 2 4
18 tháng 1 2019
Vì AH vuông góc với BC mà tam giác ABC cân tại A (gt)
Nên AH vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow BH=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)
Áp dụng định lý Pi-ta-go vào tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)
Hay \(AH^2=12^2-5^2\)
\(\Rightarrow AH^2=144-25\)
\(\Rightarrow AH^2=119\)
\(\Rightarrow AH=\sqrt{119}\)
A B C H c c 120
Kẻ AH vuông góc BC. Vì tam giác ABC cân tại A nên AH đồng thời là tia phân giác góc A
=> \(\widehat{BAH}\)= \(\widehat{CAH}\)= 60o
Tam giác BAH, có: \(\widehat{BAH}\)= 60o; \(\widehat{AHB}\)=90o
=> AH = \(\frac{1}{2}\)BA = \(\frac{1}{2}\)c ( nửa tam giác đều)
Áp dụng định lý Py-ta-go vào tam giác AHB vuông tại H, ta có:
BH2 + AH2 = AB2 <=> BH2 + \(\left(\frac{1}{2}c\right)^2\)= c2 <=> BH = \(\frac{\sqrt{3}}{2}c\)
=> BC= 2BH = \(\sqrt{3}c\)