Giúp e hứa tick ah. (Làm bài 5 thoi ah)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#)Giải :
(Hình bạn tự vẽ nhé :v)
AB cắt CD tại K
Theo bổ đề hình thang \(\Rightarrow\) K,E,F thẳng hàng
Kẻ EN//AB ta được hình bình hàng ABEN
\(\Rightarrow\) BE = AN ; \(\widehat{A}=\widehat{ENF}\) (1)
Ta có : \(\widehat{A}+\widehat{D}=90^o\Rightarrow\widehat{AKD}=90^o\)
\(\Rightarrow\Delta AKD\) vuông tại K, đường trung tuyến KF
\(\Rightarrow\widehat{A}=\widehat{AKF}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}=\widehat{ENF}=\widehat{AKF}\) (3)
Lại có : \(\widehat{AKF}=\widehat{NEF}\left(NE//AB\right)\) (4)
Từ (3) và (4) \(\Rightarrow\widehat{ENF}=\widehat{NEF}\)
\(\Rightarrow\Delta ENF\) là tam giác cân
\(\Rightarrow FN=FE\) (cặp cạnh tương ứng bằng nhau) (5)
Mà \(FN=FA-NA=\frac{AD-BC}{2}\) (6)
Từ (5) và (6) \(\Rightarrow\) đpcm

a.Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
b.AH: đã có
Áp dụng định lý pitago vào tam giác vuông AHC, có:
\(AC^2=AH^2+CH^2\)
\(\Rightarrow CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)

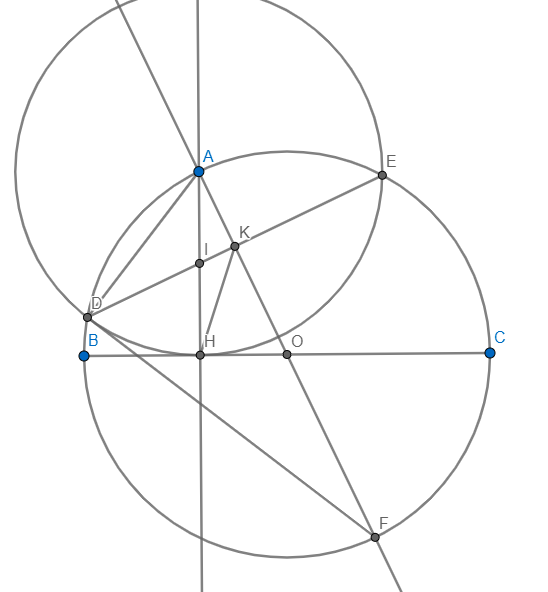
a) AO cắt (O) tại F \(\Rightarrow AF\) là đường kính \(\Rightarrow\angle ADF=90\)
Vì DE là dây chung của (A;AH) và (O) và AO là đường nối tâm
\(\Rightarrow AO\bot DE\)
Xét \(\Delta ADK\) và \(\Delta AFD:\) Ta có: \(\left\{{}\begin{matrix}\angle DAFchung\\\angle AKD=\angle ADF=90\end{matrix}\right.\)
\(\Rightarrow\Delta ADK\sim\Delta AFD\left(g-g\right)\Rightarrow\dfrac{AD}{AF}=\dfrac{AK}{AD}\Rightarrow AD^2=AF.AK\)
mà \(AF=2AO\Rightarrow AD^2=2AO.AK\)
b) Xét \(\Delta AIK\) và \(\Delta AOH:\) Ta có: \(\left\{{}\begin{matrix}\angle HAOchung\\\angle AKI=\angle AHO=90\end{matrix}\right.\)
\(\Rightarrow\Delta AIK\sim\Delta AOH\left(g-g\right)\Rightarrow\dfrac{AI}{AO}=\dfrac{AK}{AH}\Rightarrow AI.AH=AK.AO\)
\(\Rightarrow AI.AH=\dfrac{AD^2}{2}=\dfrac{AH^2}{2}\) (cùng = bán kính của (A;AH))
\(\Rightarrow AI=\dfrac{AH}{2}\Rightarrow I\) là trung điểm AH

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=10(cm)
b: Xét ΔABH vuông tại H có \(AB^2=AH^2+HB^2\)
nên HB=3,6(cm)
=>HC=BC-HB=6,4(cm)
câu này lúc nãy làm rồi em nhé! ( bổ sung BH )
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)

Diện tích hình thoi `ABCD` là:
`8xx5:2=20(cm^2)`
Đáp só: `20 \ cm^2`

[ 48 phut 36 giay : 9 ] + 9,54 phut = 5phut 24 giay + 9,54 phut = 5,4 phut + 9,54 phut = 14,94 phut

a: \(BC=\sqrt{6^2+8^2}=10\)
\(AH=\dfrac{6\cdot8}{10}=4.8\)
BH=3.6
CH=6.4