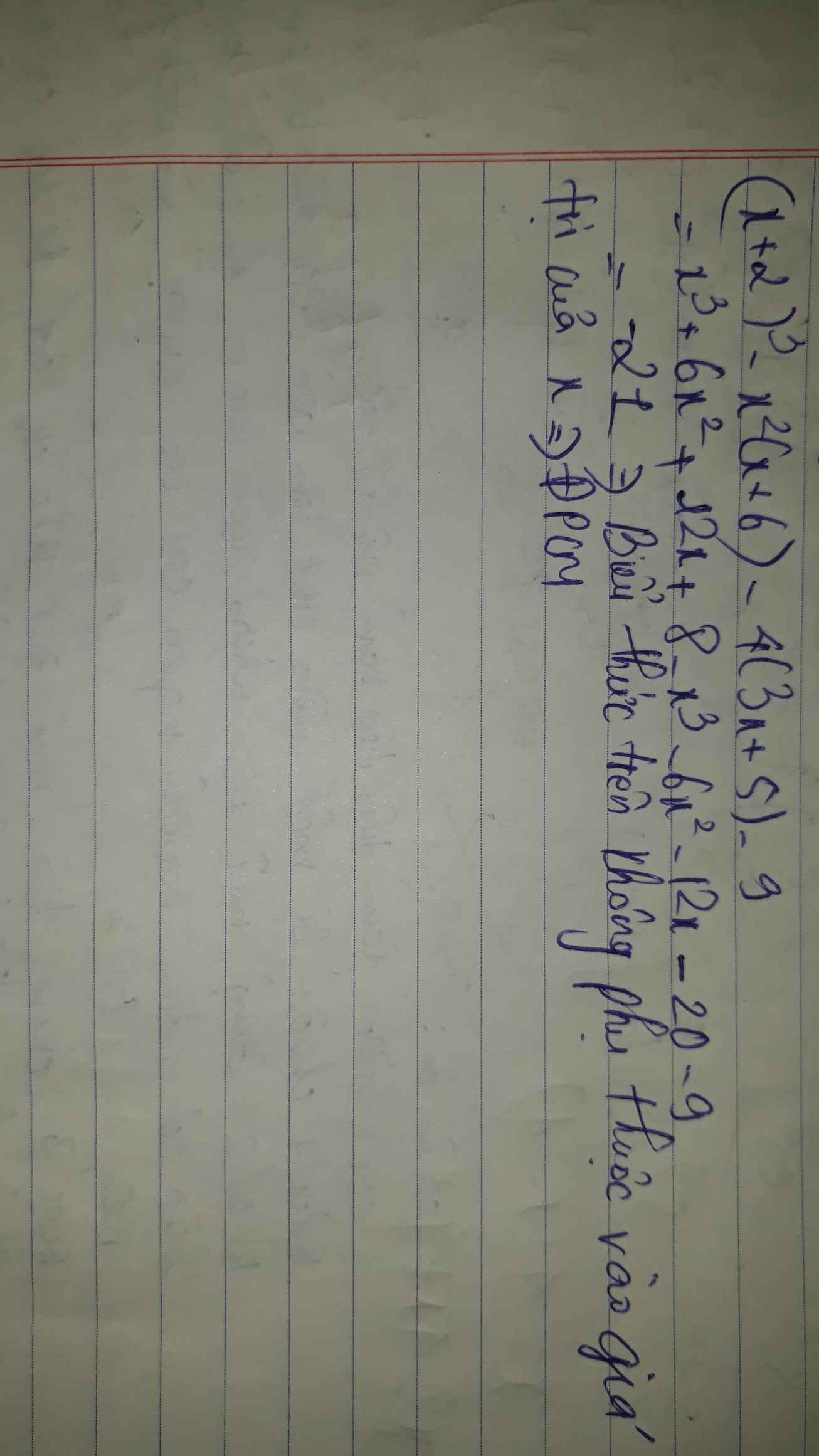Chứng minh biểu thức sau ko phụ thuộc vào x : [(x+6)^2+(x-6)^2]:(x^2+36)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A
💋Amanda💋
22 tháng 3 2020
https://i.imgur.com/wBAh2S4.jpg
Đúng(0)
Những câu hỏi liên quan
15 tháng 7 2021
A = 6( x3 + 23 ) - 6x3 - 2 = 6x3 + 48 - 6x3 - 2 = 46 ( đpcm )
DL
3 tháng 9 2019
Ta có \(x^4+y^4=\left(x^2\right)^2+\left(y^2\right)^2=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=1-2x^2y^2\)
Tương tự \(x^6+y^6=\left(x^2\right)^3+\left(y^2\right)^3=\left(x^2+y^2\right)\left(x^2+y^2-x^2y^2\right)=1-x^2y^2\)
Thế vào ta được
\(2\left(1-x^2y^2\right)-3\left(1-2x^2y^2\right)=2-2x^2y^2-3+6x^2y^2=4x^2y^2-1=\left(2xy\right)^2-1\)
Vậy là nó có phụ thuộc vào biến x,y mà bạn ? đề có sai không
8 tháng 9 2019
Dũng Lê Trí ơi bạn viết sai rồi \(\left(x^2\right)^3+\left(y^2\right)^3\)phải bằng\(\left(x^2+y^2\right)\left(x^4+y^4-x^2y^2\right)\)
20 tháng 8 2021
\(B=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+3x^2+3x+1\right)+6\left(x^2+1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6x^2-6\)
\(=-6x^2-2+6x^2-6\)
\(=-8\)
Vậy biểu thức không phụ thuộc vào biến
20 tháng 8 2021
\(B=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)
\(=-6x^2-2+6x^2-6=-8\)
Vậy biểu thức ko phụ thuộc vào giá trị biến x