mọi người giải giúp mình ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

Bài 3.
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
Gia tốc vật:
\(a=\dfrac{F-F_{ms}}{m}=\dfrac{4,5-\mu mg}{m}=\dfrac{4,5-0,2\cdot1,5\cdot10}{1,5}=1\)m/s2
Vận tốc vật sau 2s:
\(v=a\cdot t=1\cdot2=2\)m/s

Bài 3:
a, Lực hấp dẫn giữa Trái Đất và Mặt Trăng
\(F_{hd}=G\cdot\dfrac{M_1M_2}{r^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,84\cdot10^8\right)^2}=1,95\cdot10^{20}\left(N\right)\)


\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...

Đổi 100ml = 0,1 lít
Ta có: \(n_{HCl}=2.0,1=0,2\left(mol\right)\)
a. PTHH: \(AgNO_3+HCl--->AgCl\downarrow+HNO_3\)
Theo PT: \(n_{AgNO_3}=n_{HCl}=0,2\left(mol\right)\)
Đổi 200ml = 0,2 lít
=> \(C_{M_{AgNO_3}}=\dfrac{0,2}{0,2}=1M\)
b. Ta có: \(m_{dd_{HNO_3}}=0,1\left(lít\right)\)
Theo PT: \(n_{HNO_3}=n_{HCl}=0,2\left(mol\right)\)
=> \(C_{M_{HNO_3}}=\dfrac{0,2}{0,1}=2M\)

Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2



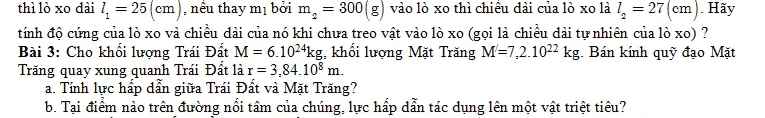
 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé 


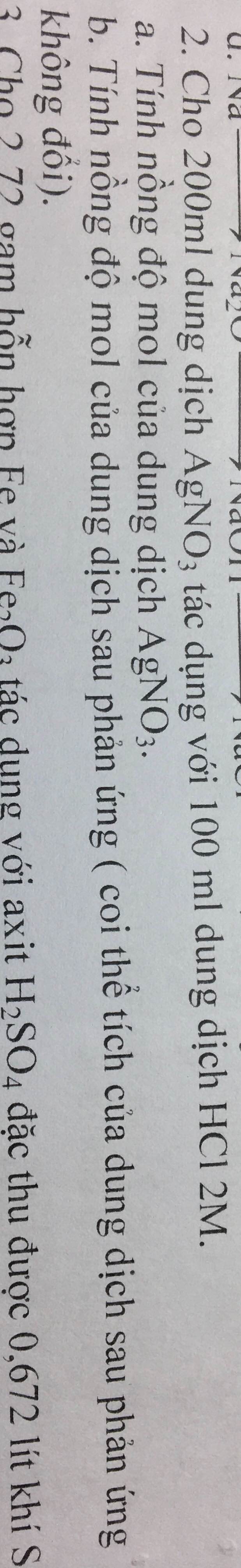


a) \(AB=AE+BE=6,4+3,6=10\left(cm\right)\)
\(\Delta ABC\)vuông tại A có đường cao AH nên \(\hept{\begin{cases}AH^2=AE.AB\\BH^2=BE.AB\end{cases}\Rightarrow\hept{\begin{cases}AH=\sqrt{AE.AB}=\sqrt{6,4.10}=\sqrt{64}=8\left(cm\right)\\BH=\sqrt{BE.AB}=\sqrt{3,6.10}=\sqrt{36}=6\left(cm\right)\end{cases}}}\)
Vậy \(S_{ABH}=\frac{AH.BH}{2}=\frac{8.6}{2}=24\left(cm^2\right)\)
b) Ta có: \(AH^2=AE.AB\left(cmt\right)\)
Mà \(\Delta ACH\)vuông tại H có đường cao HF nên \(AH^2=AF.AC\left(htl\right)\)
Từ đó ta có: \(AE.AB=AF.AC\left(=AH^2\right)\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\)
Xét \(\Delta AEF\)và \(\Delta ACB\), ta có:
\(\frac{AE}{AC}=\frac{AF}{AB}\left(cmt\right);\widehat{BAC}chung\)
\(\Rightarrow\Delta AEF\)~ \(\Delta ACB\)(c.g.c)
c) \(\Delta ACH\)vuông tại H nên \(\sin C=\frac{AH}{AC}\Rightarrow\sin^2C=\frac{AH^2}{AC^2}=\frac{AF.AC}{AC^2}=\frac{AF}{AC}\)
Vậy đẳng thức được chứng minh.
d) Vì \(\Delta ABH\)và \(\Delta ACH\)là các tam giác vuông tại H
\(\Rightarrow\hept{\begin{cases}\sin B=\frac{AH}{AB}\Rightarrow\sin^2B=\frac{AH^2}{AB^2}\\\sin C=\frac{AH}{AC}\Rightarrow\sin^2C=\frac{AH^2}{AC^2}\end{cases}}\)
\(\sin^2B.\sin^2C=\frac{AH^2.AH^2}{AB^2.AC^2}=\frac{AE.AB.AF.AC}{AB^2.AC^2}=\frac{AE.AF}{AB.AC}=\frac{AE}{AC}.\frac{AF}{AB}\)
Vì \(\Delta AEF\)~\(\Delta ABC\)(cmt) \(\Rightarrow\hept{\begin{cases}\frac{S_{AEF}}{S_{ABC}}=\left(\frac{AE}{AC}\right)^2\\\frac{AE}{AC}=\frac{AF}{AB}\end{cases}}\)
\(\Rightarrow\sin^2B.\sin^2C=\frac{AE}{AC}.\frac{AF}{AB}=\frac{AE}{AC}.\frac{AE}{AC}=\left(\frac{AE}{AC}\right)^2=\frac{S_{AEF}}{S_{ABC}}\)
Vậy đẳng thức được chứng minh.