phương trình vô nghiệm có kí hiệu là
S=0
S=R
{KHrỗng}
Khrỗng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LS
2
DA
2
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
Nếu $x\geq 0$ thì: $|-3x|=3x$. PT trở thành:
$4x+5=3x\Leftrightarrow x=-5<0$ (loại vì $x\geq 0$)
Nếu $x<0$ thì $|-3x|=-3x$. PT trở thành:
$4x+5=-3x\Leftrightarrow x=\frac{-5}{7}$ (thỏa mãn)
Vậy tập nghiệm của pt là $\left\{\frac{-5}{7}\right\}$
DA
1
10 tháng 5 2021
`|4x+4|=|-3x|`
`<=>` $\left[ \begin{array}{l}4x+4=-3x\\4x+1=3x\end{array} \right.$
`<=>` $\left[ \begin{array}{l}7x=-4\\x=-1\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=\dfrac{-4}{7}\\x=-1\end{array} \right.$
Vậy `S={-1,-4/7}`
DA
2
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
Nếu $x\geq 0$ thì $|-2x|=2x$. PT trở thành:
$3x+1=2x\Leftrightarrow x=-1<0$ (loại)
Nếu $x< 0$ thì $|-2x|=-2x$. PT trở thành:
$3x+1=-2x\Leftrightarrow x=-\frac{1}{5}$ (thỏa mãn)
Vậy tập nghiệm của pt là $S=\left\{\frac{-1}{5}\right\}$
DA
1
J
11 tháng 5 2021
-7x +3 = |3x|
\(\Leftrightarrow\left[{}\begin{matrix}-7x+3=3xkhi3x\ge0\\-7x+3=-3xkhi3x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-7x-3x=-3khix\ge0\\-7x+3x=-3khix< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-10x=-3khix\ge0\\-4x=-3khix< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{10}khix\ge0\left(1\right)\\x=\dfrac{3}{4}khix< 0\left(2\right)\end{matrix}\right.\)
trường hợp (1) thỏa mãn,
trường hợp (2) không thỏa mãn.
Vậy S ={ \(\dfrac{3}{10}\)}
CM
3 tháng 4 2019
Chọn D.
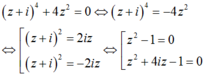
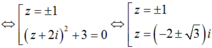
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
CM
21 tháng 10 2018
8x2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b2 – 4ac = (-1)2 – 4.8.1 = -31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
CM
19 tháng 6 2018
5x2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b2 – 4ac = (-1)2 – 4.5.(-35) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x1 + x2 = -b/a = 1/5
x1.x2 = c/a = -35/5 = -7.
CM
2 tháng 11 2017
2x2 – 17x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b2 – 4ac = (-17)2 – 4.2.1 = 281 > 0.
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x1 + x2 = -b/a = 17/2
x1.x2 = c/a = 1/2.
Kí hiệu là S