Giải phương trình : x2 - 2x = -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
1
AH
Akai Haruma
Giáo viên
15 tháng 5 2021
Lời giải:
PT $\Leftrightarrow (x^2-1)^3+(x^2+2)^3+(2x-1)^3-3(x^2-1)(x^2+2)(2x-1)=0$
Đặt $x^2-1=a; x^2+2=b; 2x-1=c$ thì pt trở thành:
$a^3+b^3+c^3-3abc=0$
$\Leftrightarrow (a+b)^3+c^3-3ab(a+b)-3abc=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Nếu $a+b+c=0$
$\Leftrightarrow x^2-1+x^2+2+2x-1=0$
$\Leftrightarrow 2x^2+2x=0$
$\Rightarrow x=0$ hoặc $x=-1$
Nếu $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$ (dễ CM)
$\Leftrightarrow a=b=c$
$\Leftrightarrow x^2-1=x^2+2=2x-1$ (vô lý)
Vậy..........
15 tháng 5 2021
Akai Haruma Chị ơi chỗ
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\) từ chỗ trên chị tách làm sao ra được vế beeb phải vậy ạ
4 tháng 9 2023
\(x^2-2x=2\sqrt{2x-1}\left(đk:x\ge0,5\right)\\ \Leftrightarrow x^4-4x^3+4x^2=4\left(2x-1\right)\\ \Leftrightarrow x^4-4x^3+4x^2=8x-4\\ \Leftrightarrow x^4-4x^3+4x^2-8x+4=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2+\sqrt{2}\left(tm\right)\\x=2-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{2-\sqrt{2};2+\sqrt{2}\right\}\)
PN
1
MH
12 tháng 12 2023
\(x^2-2x=2\sqrt{2x-1}\) \(\left(Đk:x\ge\dfrac{1}{2}\right)\)
\(x^2=2x+2\sqrt{2x-1}\)
\(x^2=2x-1+2\sqrt{2x-1}+1\)
\(x^2=\left(\sqrt{2x-1}+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2x-1}+1\\x=-\sqrt{2x-1}-1\end{matrix}\right.\)
+) \(x=\sqrt{2x-1}+1\)
\(x-1=\sqrt{2x-1}\left(x\ge1\right)\)
\(x^2-2x+1=2x-1\)
\(x^2-4x+2=0\)
\(\left(x-2\right)^2=2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2}+2\left(TM\right)\\x=2-\sqrt{2}\left(L\right)\end{matrix}\right.\)
+) \(x=-\sqrt{2x-1}-1\)
VP\(\le-1\) mà \(VT\ge\dfrac{1}{2}\)
=> phương trình vô nghiệm
Vậy \(S=\left\{2+\sqrt{2}\right\}\)
CM
2 tháng 7 2017
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
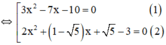
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
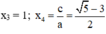
Vậy phương trình có tập nghiệm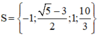 
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
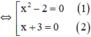
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
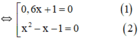
+ Giải (1): 0,6x + 1 = 0 ⇔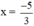 
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm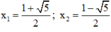 
Vậy phương trình có tập nghiệm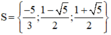 
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
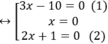
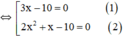
+ Giải (1): 3x – 10 = 0 ⇔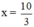 
+ Giải (2):
PT
1
CM
24 tháng 11 2018
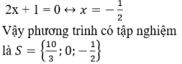
Điều kiện của phương trình là x 2 - 2 x + 3 > 0
Bình phương hai vế ta được phương trình hệ quả.
x 2 - 2 x + 3 = 4 x 2 - 4 x + 1
⇔ 3 x 2 - 2 x - 2 = 0
Phương trình cuối có hai nghiệm 
. Khi thay các giá trị này vào phương trình ban đầu thì giá trị 
bị loại.
Đáp số: 
TN
0
1N
1
14 tháng 6 2023
A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-x1x2
=(1/2)^2-(-1/4)=1/4+1/4=1/2
DN
2
28 tháng 2 2022
\(\Leftrightarrow2x^3-2x+x^2-1-4x^2+2x+2=0\)
\(\Leftrightarrow2x^3-3x^2+1=0\)
\(\Leftrightarrow2x^3-2x^2-x^2+1=0\)
\(\Leftrightarrow2x^2\left(x-1\right)-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-2x+x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(2x+1\right)=0\)
=>x=1 hoặc x=-1/2
28 tháng 2 2022
\(\left(2x+1\right)\left(x^2-1\right)=4x^2-2x-2\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=4x^2-4x+2x-2\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=4x\left(x-1\right)+2\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=\left(4x+2\right)\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=2\left(2x+1\right)\left(x-1\right)\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)-2\left(2x+1\right)\left(x-1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(x-1\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
23 tháng 2 2021
tham khảo
https://hoidapvietjack.com/q/57243/giai-cac-phuong-trinh-sau-a-2x12-2x-12-b-x2-3x-2-5x2-3x60
TM
23 tháng 2 2021
b) (2x+1)2-2x-1=2
\(< =>4x^2+4x+1-2x-1=2\)
\(< =>4x^2+2x-2=0\)
\(< =>4x^2+4x-2x-2=0\)
\(< =>\left(4x^2+4x\right)-\left(2x+2\right)=0\)
\(< =>4x\left(x+1\right)-2\left(x+1\right)=0\)
\(< =>\left(x+1\right)\left(4x-2\right)=0\)
\(=>\left\{{}\begin{matrix}x+1=0=>x=-1\\4x-2=0=>x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy....
\(^{x^2-2x=-1\Leftrightarrow x^2-2x+1=0\Leftrightarrow x=1}\)
x2 - 2x = -1
<=> x2 - 2x + 1 = 0
<=> x2 - 2( x )( 1 ) + 1 = 0
<=> ( x - 1 )2 = 0
<=> x - 1 = 0
<=> x = 1