Tìm giới hạn :
K
Khách
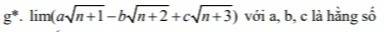
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 3 2019
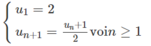
Ta có
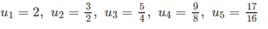
Dự đoán
Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
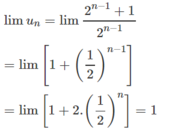
\(\lim\limits_{x\rightarrow0}\dfrac{2\sqrt{x+1}-\sqrt{4-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{4\left(x+1\right)-\left(4-x\right)}{x\left(2\sqrt{x+1}+\sqrt{4-x}\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{5x}{x\left(2\sqrt{x+1}+\sqrt{4-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{5}{2\sqrt{x+1}+\sqrt{4-x}}=\dfrac{5}{4}\)
KB
2 tháng 4 2022
Ta có : \(A=lim_{x\rightarrow1}\dfrac{\sqrt{2x-1}-x}{x^2-1}=lim_{x\rightarrow1}\dfrac{2x-1-x^2}{\left(x^2-1\right)\left(\sqrt{2x-1}+x\right)}\) \(=lim_{x\rightarrow1}\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)\left(\sqrt{2x-1}+x\right)}\) \(=lim_{x\rightarrow1}\dfrac{1-x}{\left(x+1\right)\left(\sqrt{2x-1}+x\right)}=0\)
14 tháng 8 2023
Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
14 tháng 8 2023
Dễ thấy ��>0,∀�∈N∗un>0,∀n∈N∗.
Ta có ��+1−��=��2+20212��−��=2021−��22��un+1−un=2unun2+2021−un=2un2021−un2
Với �≥2n≥2 thì ��=��−12+20212��−1un=2un−1un−12+2021 =��−12+20212��−1=2un−1+2un−12021 >2��−12.20212��−1>22un−1.2un−12021 =2021=2021
Vậy ��>2021,∀�≥2un>2021,∀n≥2, suy ra ��+1−��=2021−��22��<0,∀�∈N∗un+1−un=2un2021−un2<0,∀n∈N∗
⇒⇒ Dãy (��)(un) là dãy giảm. Mà ��>2021un>2021 ⇒(��)⇒(un) có giới hạn hữu hạn. Đặt lim�→+∞��=�n→+∞limun=L ⇒�=�2+20212�⇒L=2LL2+2021 ⇔�=2021⇔L=2021
Vậy lim�→+∞��=2021n→+∞limun=2021
