Giúp mình câu 8, ảnh ở dưới phần bình luận
#Sở_aka_Py
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
P
_Py_(1m4)_sập_nghiệp
11 tháng 3 2020
https://i.imgur.com/5SGu1Xc.jpg
Đúng(0)
Những câu hỏi liên quan
PT
2
15 tháng 10 2023
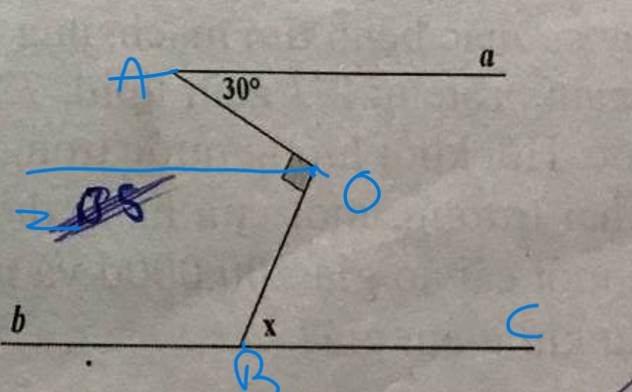
Qua O, kẻ tia Oz//Aa
Oz//Aa
Aa//BC
Do đó: Oz//BC
Oz//Aa
=>\(\widehat{zOA}=\widehat{OAa}\)(hai góc so le trong)
=>\(\widehat{zOA}=30^0\)
\(\widehat{zOA}+\widehat{zOB}=\widehat{AOB}=90^0\)
=>\(\widehat{zOB}=90^0-30^0=60^0\)
Oz//BC
=>\(\widehat{zOB}=\widehat{OBC}\)(hai góc so le trong)
=>\(x=60^0\)
PT
3
15 tháng 10 2023
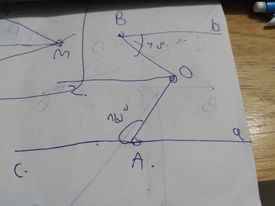
Đặt tên các điểm, các tên đường thẳng như trên hình vẽ.
Qua O, kẻ tia Oz//Bb(Oz và Bb là hai tia nằm ở hai phía khác nhau)
Oz//Bb
=>\(\widehat{zOB}=\widehat{bBO}\)(hai góc so le trong)
=>\(\widehat{zOB}=40^0\)
Oz//Bb
Bb//Ac
=>Oz//Ac
=>\(\widehat{zOA}+\widehat{OAc}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zOA}=180^0-120^0=60^0\)
\(\widehat{BOA}=\widehat{zOB}+\widehat{zOA}=60^0+40^0=100^0\)
PT
2
15 tháng 10 2023
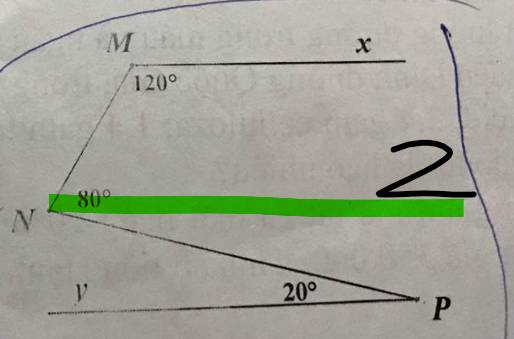
Qua N, kẻ tia Nz//Mx
Nz//Mx
=>\(\widehat{zNM}+\widehat{M}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zNM}=60^0\)
\(\widehat{zNM}+\widehat{zNP}=\widehat{MNP}\)
=>\(\widehat{zNP}=80^0-60^0=20^0\)
\(\widehat{zNP}=\widehat{P}\)
mà hai góc này ở vị trí so le trong
nên Nz//Py
=>Mx//Py
TS
3
PA
2
21 tháng 7 2023
d: \(=\dfrac{-9\sqrt{3}-6\sqrt{2}}{19}-\dfrac{\sqrt{3}}{5}\)
\(=\dfrac{-64\sqrt{3}-30\sqrt{2}}{95}\)
b: \(=\dfrac{37\left(7-2\sqrt{3}\right)}{49-12}=7-2\sqrt{3}\)
PT
2
9 tháng 11 2023
\(M=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
=>\(2M=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}\)
=>\(2M-M=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)
=>\(M=1-\dfrac{1}{2^{100}}< 1\)
HL
3
8 tháng 12 2023
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)