S = 3 - 32 + 33 - 34 + .... + 319 - 320
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
1
PT
1
NH
1
CH
14 tháng 11 2023
3A = 3+32+33+34+...+320+321
3A - A = (3+32+33+34+...+320+321) - ( 1+3+32+33+...+319+220)
2A = 321-1
A = \(\dfrac{31^{21}-1}{2}\)
NN
14 tháng 8 2023
1.
a.\(A=1+2^1+2^2+2^3+...+2^{2007}\)
\(2A=2+2^2+2^3+....+2^{2008}\)
b. \(A=\left(2+2^2+2^3+...+2^{2008}\right)-\left(1+2^1+2^2+..+2^{2007}\right)\)
\(=2^{2008}-1\) (bạn xem lại đề)
2.
\(A=1+3+3^1+3^2+...+3^7\)
a. \(2A=2+2.3+2.3^2+...+2.3^7\)
b.\(3A=3+3^2+3^3+...+3^8\)
\(2A=3^8-1\)
\(=>A=\dfrac{2^8-1}{2}\)
3
.\(B=1+3+3^2+..+3^{2006}\)
a. \(3B=3+3^2+3^3+...+3^{2007}\)
b. \(3B-B=2^{2007}-1\)
\(B=\dfrac{2^{2007}-1}{2}\)
4.
Sửa: \(C=1+4+4^2+4^3+4^4+4^5+4^6\)
a.\(4C=4+4^2+4^3+4^4+4^5+4^6+4^7\)
b.\(4C-C=4^7-1\)
\(C=\dfrac{4^7-1}{3}\)
5.
\(S=1+2+2^2+2^3+...+2^{2017}\)
\(2S=2+2^2+2^3+2^4+...+2^{2018}\)
\(S=2^{2018}-1\)
14 tháng 8 2023
4:
a:Sửa đề: C=1+4+4^2+4^3+4^4+4^5+4^6
=>4*C=4+4^2+...+4^7
b: 4*C=4+4^2+...+4^7
C=1+4+...+4^6
=>3C=4^7-1
=>\(C=\dfrac{4^7-1}{3}\)
5:
2S=2+2^2+2^3+...+2^2018
=>2S-S=2^2018-1
=>S=2^2018-1
HK
5
16 tháng 1 2022
\(S=1+3+3^2+3^3+...+3^8+3^9\)
\(=1+3+3^2\left(1+3\right)+...+3^8\left(1+3\right)\)
\(=4\left(1+3^2+...+3^8\right)⋮4\)
16 tháng 1 2022
\(S=\left(1+3\right)+3^2\left(1+3\right)+...+3^8\left(1+3\right)=4\left(1+3^2+...+3^8\right)⋮4\)
22 tháng 8 2021
Ta có: \(A=3+3^2+3^3+...+3^{20}\)
\(\Leftrightarrow3\cdot A=3^2+3^3+3^4+...+3^{21}\)
\(\Leftrightarrow2\cdot A=3^{21}-3\)
hay \(A=\dfrac{3^{21}-3}{2}\)
VG
1
TT
1
18 tháng 12 2021
\(S=\left(1+3\right)+...+3^8\left(1+3\right)=4\left(1+...+3^8\right)⋮4\)
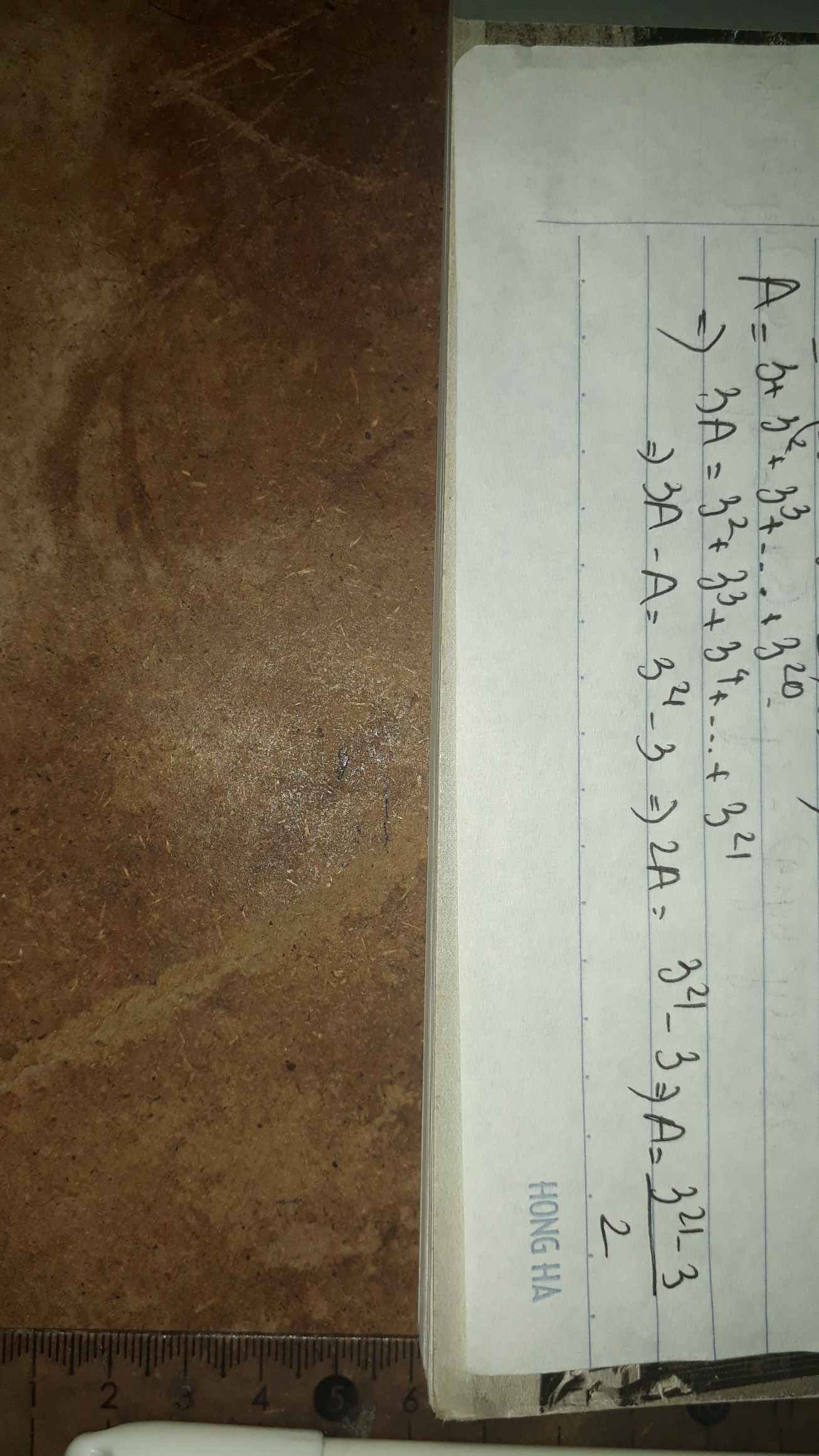
S = 3 - 32 + 33 - 34 + .... + 319 - 320
3S = 32 - 33 + 34 - 35 + . . . + 320 - 321
2S = 3 - 321
S = \(\frac{3}{2}-\frac{3^{21}}{2}\)