Giải pt sau: 2(x-1)x-a(x-1)=2a+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2017
1) Nhìn cái pt hết ham, nhưng bấm nghiệm đẹp v~`~
\(\left(\sqrt{2}+2\right)\left(x\sqrt{2}-1\right)=2x\sqrt{2}-\sqrt{2}\)
\(\Leftrightarrow\left(\sqrt{2}+2\right)\left(x\sqrt{2}-1\right)-2x\sqrt{2}+\sqrt{2}=0\)
\(\Leftrightarrow2x-\sqrt{2}+2x\sqrt{2}-2-2x\sqrt{2}+\sqrt{2}=0\)
\(\Leftrightarrow2x-2=0\Leftrightarrow2x=2\Rightarrow x=1\)
20 tháng 1 2017
2a^4=(1-a)^2=a^2-2a+1
\(A=\frac{2a-3}{\sqrt{2\left(a^2-4a+4\right)}+2a^2}=\frac{2a-3}{\sqrt{2}!\left(a-2\right)!+2a^2}\)a> 2 không thể là nghiệm=> a<2
\(A=\frac{2a-3}{\sqrt{2}\left(2-a\right)+2a^2}=\frac{2a-3}{2a^2-\sqrt{2}a+2\sqrt{2}}=\frac{2a-3}{\sqrt{2}\left(\sqrt{2}a^2-a-1+3\right)}\)
\(A=\frac{2a-3}{\sqrt{2}\left(3\right)}\)
22 tháng 4 2021
a) ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Ta có: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra: \(x^2+3x+2-5x+10=12+x^2-4\)
\(\Leftrightarrow x^2-2x+12-8-x^2=0\)
\(\Leftrightarrow-2x+4=0\)
\(\Leftrightarrow-2x=-4\)
hay x=2(loại)
Vậy: \(S=\varnothing\)
22 tháng 4 2021
b) Ta có: \(\left|2x+6\right|-x=3\)
\(\Leftrightarrow\left|2x+6\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=x+3\left(x\ge-3\right)\\-2x-6=x+3\left(x< -3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-x=3-6\\-2x-x=3+6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\)
Vậy: S={-3}
14 tháng 7 2020
Ta có : \(ax^2+3\left(a+1\right)x+2a+4=0\left(a=a;b=3a+3;c=2a+4\right)\)
Theo hệ thức Vi et ta có : \(x_1+x_2=\frac{-3a-3}{a};x_1x_1=\frac{2a+4}{a}\)
Theo bài ra ta có : \(x_1^2+x_2^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\) Thay vào ta đc :
\(\Leftrightarrow\left(\frac{-3a-3}{a}\right)^2-2\left(\frac{2a+4}{a}\right)=4\)
\(\Leftrightarrow\frac{9\left(a+1\right)^2}{a^2}-\frac{4a+8}{a}=4\Leftrightarrow\frac{9\left(a+1\right)^2}{a^2}-\frac{4a^2+8a}{a^2}=\frac{4a^2}{a^2}\)
Khử mẫu ta đc : \(9\left(a+1\right)^2-4a^2+8a=4a^2\)
\(\Leftrightarrow9\left(a^2+2a+1\right)-4a^2+8a=4a^2\)
\(\Leftrightarrow9a^2+18a+9-4a^2+8a-4a^2=0\)
\(\Leftrightarrow a^2+27a+9=0\)Ta có : \(\Delta=27^2-4.9=729-36=613>0\)
Nên phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-27-\sqrt{613}}{2};x_2=\frac{-27+\sqrt{613}}{2}\)
KN
5 tháng 3 2020
a) \(2\left(x-1\right)-a\left(x-1\right)=2a+3\)
\(\Leftrightarrow2a-2-ax+a=2a+3\)
\(\Leftrightarrow-2-ax+a=3\)
\(\Leftrightarrow-a\left(x-1\right)=5\)
\(\Leftrightarrow\left(x-1\right)=\frac{-5}{a}\Leftrightarrow x=\frac{a-5}{a}\)
KN
5 tháng 3 2020
b) \(\frac{x+1}{2}+\frac{x+2}{3}+\frac{x+3}{4}=3\)
\(\Leftrightarrow\frac{12x+12+8x+16+6x+18}{24}=3\)
\(\Leftrightarrow12x+12+8x+16+6x+18=72\)
\(\Leftrightarrow26x+46=72\)
\(\Leftrightarrow26x=26\Leftrightarrow x=1\)
22 tháng 4 2022
Bài 1:
c) |2x - 1| = x + 2
<=> 2x - 1 = +(x + 2) hoặc -(x + 2)
* 2x - 1 = x + 2
<=> 2x - x = 2 + 1
<=> x = 3
* 2x - 1 = -(x + 2)
<=> 2x - 1 = x - 2
<=> 2x - x = -2 + 1
<=> x = -1
Vậy.....
29 tháng 4 2020
a) với a = -2 ta được phương trình:
3.[(-2) - 2].x + 2.(-2).(x - 1) = 4.(-2) + 3
<=> 3.(-4x) - 4.(x - 1) = (-8) + 3
<=> -12x - 4(x - 1) = -5
<=> -12x - 4x + 4 = -5
<=> -16x + 4 = -5
<=> -16x = -5 - 4
<=> -16x = -9
<=> x = 9/16
b) để x = 1, ta có:
3.(a - 2).1 + 2a(1 - 1) = 4a + 3
<=> 3(a - 2) + 0 = 4a + 3
<=> 3a - 6 = 4a + 3
<=> 3a - 6 - 4a = 3
<=> -a - 6 = 3
<=> -a = 3 + 6
<=> a = -9
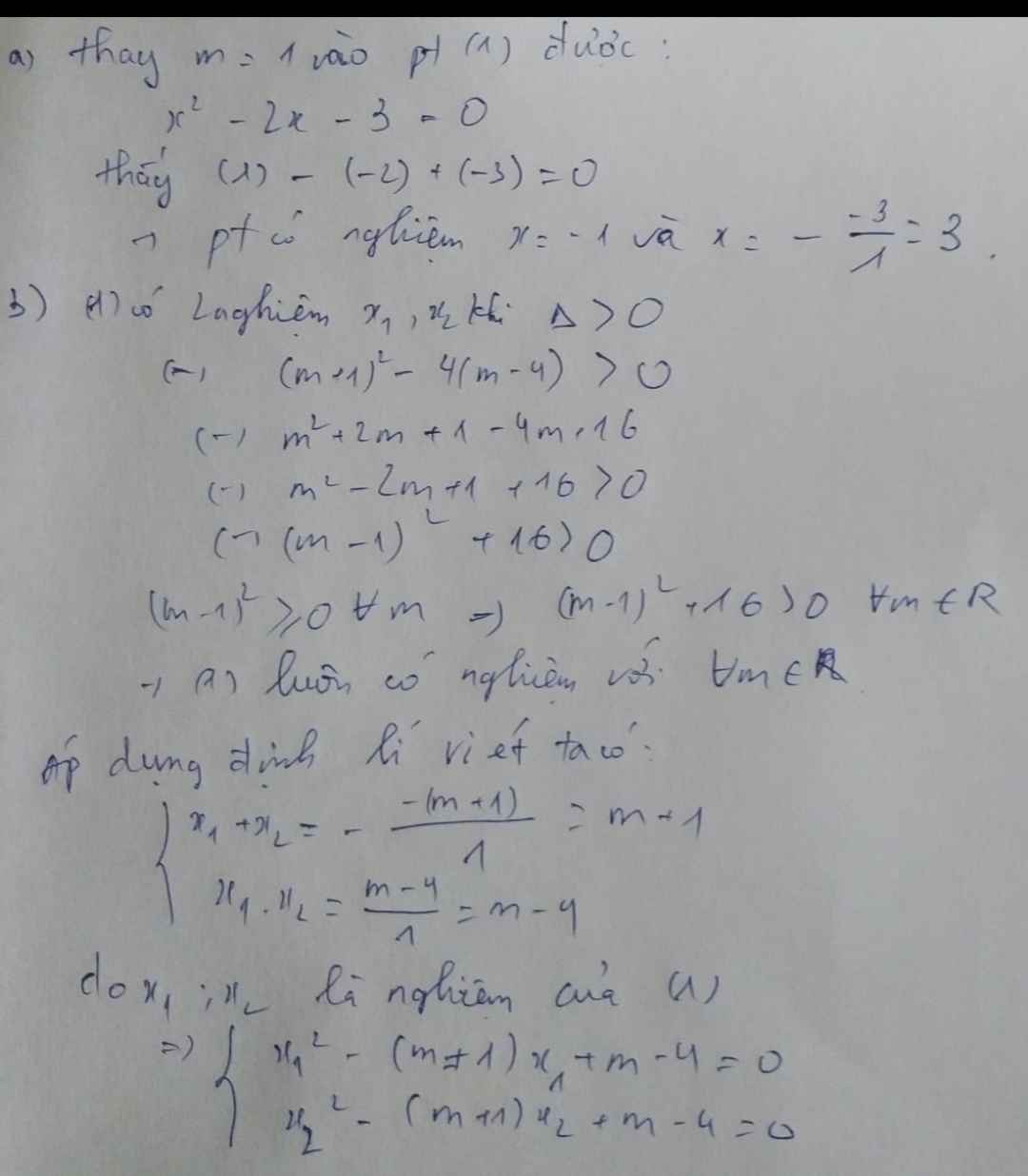
Sửa \(2\left(a-1\right)x-a\left(x-1\right)=2a+3\)
\(2x\left(a-1\right)-a\left(x-1\right)=2a+3\)
\(2xa-2x-ax+a=2a+3\)
\(ax-2x=2a+3-a\)
\(ax-2x=a+3\)
\(x\left(a-2\right)=a+3\)
Vậy pt cs nghiệm \(x=\frac{a+3}{a-2}\)