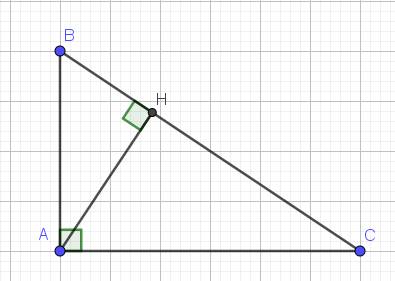
Cho tam giác ABC. Biết AB = 12, AC = 16, BC = 20, AH là đường cao. a) Tính AH b) C/m: AH2 = HB.HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 4 2023
a: Xet ΔABC vuông tại A co AH là đường cao
nên AH^2=HB*HC
b: BC=3,6+6,4=10cm
\(AH=\sqrt{3.6\cdot6.4}=4.8\left(cm\right)\)
\(AB=\sqrt{3.6\cdot10}=6\left(cm\right)\)
=>AC=8cm
15 tháng 4 2019
Bạn kham khảo link này nhé.
Câu hỏi của Trần Ngô Anh Tuyền - Toán lớp 8 - Học toán với OnlineMath
30 tháng 4 2023
a: Xet ΔABC và ΔHBA có
góc B chung
góc BAC=góc BHA
=>ΔABC đồg dạng với ΔHBA
b: ΔABC vuông tại A mà AH là đường cao
nên HA^2=HB*HC
c: Xet ΔCAD vuông tại A và ΔCHE vuông tai H co
góc ACD=góc HCE
=>ΔCAD đồng dạng với ΔCHE
=>\(\dfrac{S_{CAD}}{S_{CHE}}=\left(\dfrac{CA}{CH}\right)^2=\left(\dfrac{8}{6,4}\right)^2=\left(\dfrac{5}{4}\right)^2=\dfrac{25}{16}\)
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Lời giải:
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
Ta có:
$AB.AC=AH.BC$ (cùng bằng 2 lần diện tích tam giác $ABC$)
b.
Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ góc $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$
$\Rightarrow AH^2=BH.CH$.
NN
9 tháng 6 2021
Xét tứ giác ABKC có:
\(B\chi\perp AB\) (gt)
\(AC\perp AB\) (gt)
\(\Rightarrow B\chi\text{//}AC\)
\(\Rightarrow\text{Tứ giác ABKC}\) là hình thang
mà \(\widehat{A}=\widehat{B}=\)\(90^0\)
Vậy hình thang ABKC là hình thang vuông
b) Xét ΔABK và ΔCHA có:
\(\widehat{ABK}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAK}=\widehat{HCA} \) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\text{ΔABK}\) \(\sim\)ΔCHA (gg)
\(\Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{CA}\)
\(\Rightarrow AB.CA=AK.CH\)
c) Xét ΔAHB và ΔCHA có:
\(\widehat{AHB}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(gg\right)\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
\(\Rightarrow AH.AH=BH.CH\)
\(\Rightarrow AH^2=BH.CH\)
\(\Rightarrow AH^2=9.16\)
\(\Rightarrow AH=12\left(cm\right)\)
Xét \(\Delta AHB\) vuông tại H có:
\(AB^2=BH^2+HA^2\) ( Định lí Pitago)
\(\Rightarrow AB^2=9^2+12^2\)
\(\Rightarrow AB=\sqrt{225=15\left(cm\right)}\)
17 tháng 4 2023
a: ΔACB vuông tại A
mà AH là đường cao
nên AH^2=HB*HC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
CD là phân giác
=>DA/AC=DB/CB
=>DA/4=DB/5=6/9=2/3
=>DA=8/3cm
=>\(CD=\sqrt{8^2+\left(\dfrac{8}{3}\right)^2}=\dfrac{8}{3}\sqrt{10}\)
Xét ΔHCI vuông tại H và ΔACD vuông tại A có
góc HCI=góc ACD
=>ΔHCI đồng dạng với ΔACD
=>CI/CD=HC/AC
=>\(\dfrac{CI}{\dfrac{8}{3}\sqrt{10}}=\dfrac{6.4}{8}=\dfrac{4}{5}\)
=>\(CI=\dfrac{32}{15}\sqrt{10}\left(cm\right)\)
sin ACH=AB/BC=3/5
=>góc ACH=37 độ
=>góc ACI=18,5 độ
\(S_{ACI}=\dfrac{1}{2}\cdot\dfrac{32}{15}\sqrt{10}\cdot8\cdot sin18.5^0\simeq8,56\left(cm^2\right)\)
MH
12 tháng 5 2022
(Tự vẽ hình)
a) Xét \(\Delta AHB\) và \(\Delta CAB\) có:
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta AHB\sim\Delta CAB\) (g.g)
b) Áp dụng định lý Pytago có:
\(BC^2=AB^2+AC^2=8^2+6^2=100\Rightarrow BC=10\left(cm\right)\)
Do \(\Delta AHB\sim\Delta CAB\Rightarrow\left\{{}\begin{matrix}\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\\\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\end{matrix}\right.\)
c) Xét \(\Delta AHB\) và \(\Delta CHA\) có:
\(\widehat{AHB}=\widehat{CHA}=90^0\)
\(\widehat{ABH}=\widehat{CAH}\) (cùng phụ \(\widehat{BAH}\))
\(\Rightarrow\Delta AHB\sim\Delta CHA\) (g.g) \(\Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\Rightarrow AH^2=BH.CH\)
9 tháng 3 2023
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot AH\cdot BC\)
=>AB*AC=AH*CB
b: Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=HC*BC
c: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC