(5x-4)2+3(16-25x2)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`1,(4x^3+3x^3):x^3+(15x^2+6x):(-3x)=0`
`<=> 4 + 3 + (-5x) + (-2)=0`
`<=> -5x+5=0`
`<=>-5x=-5`
`<=>x=1`
`2,(25x^2-10x):5x +3(x-2)=4`
`<=> 5x - 2 + 3x-6=4`
`<=> 8x -8=4`
`<=> 8x=12`
`<=>x=12/8`
`<=>x=3/2`
`3,(3x+1)^2-(2x+1/2)^2=0`
`<=> [(3x+1)-(2x+1/2)][(3x+1)+(2x+1/2)]=0`
`<=>( 3x+1-2x-1/2)(3x+1+2x+1/2)=0`
`<=>( x+1/2) (5x+3/2)=0`
`@ TH1`
`x+1/2=0`
`<=>x=0-1/2`
`<=>x=-1/2`
` @TH2`
`5x+3/2=0`
`<=> 5x=-3/2`
`<=>x=-3/2 : 5`
`<=>x=-15/2`
`4, x^2+8x+16=0`
`<=>(x+4)^2=0`
`<=>x+4=0`
`<=>x=-4`
`5, 25-10x+x^2=0`
`<=> (5-x)^2=0`
`<=>5-x=0`
`<=>x=5`

a) Ta có: \(\left(x+2\right)\left(x^2-2x+4\right)=35\)
\(\Leftrightarrow x^3+8=35\)
\(\Leftrightarrow x^3=27\)
hay x=3
b) Ta có: \(\left(25x^2+5x+1\right)\left(5x-1\right)=-9\)
\(\Leftrightarrow125x^3-1=-9\)
\(\Leftrightarrow125x^3=-8\)
\(\Leftrightarrow x=-\dfrac{2}{5}\)

Ta có:
\(P=\dfrac{5x-4y}{5x+4y}\)
\(\Leftrightarrow P^2=\left(\dfrac{5x-4y}{5x+4y}\right)^2\)
\(\Leftrightarrow P^2=\dfrac{\left(5x-4y\right)^2}{\left(5x+4y\right)^2}\)
\(\Leftrightarrow P^2=\dfrac{\left(5x\right)^2-2\cdot5x\cdot4y+\left(4y\right)^2}{\left(5x\right)^2+2\cdot5x\cdot4y+\left(4y\right)^2}\)
\(\Leftrightarrow P^2=\dfrac{\left(25x^2+16y^2\right)-40xy}{\left(25x^2+16y^2\right)+40xy}\)
Thay \(25x^2+16y^2=50xy\) vào ta có:
\(P^2=\dfrac{50xy-40xy}{50xy+40xy}=\dfrac{10xy}{90xy}=\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\)
Mà: \(4y< 5x< 0\)
Nên: \(P=\dfrac{5x-4y}{5x+4y}< 0\)
Vậy: \(P=-\dfrac{1}{3}\)
25x^2+16y^2=50xy
=>25x^2-50xy+16y^2=0
=>25x^2-10xy-40xy+16y^2=0
=>5x(5x-2y)-8y(5x-2y)=0
=>(5x-2y)(5x-8y)=0
=>5x=2y hoặc 5x=8y
5x>4y
=>5x=8y
=>x/8=y/5=k
=>x=8k; y=5k
\(P=\dfrac{5\cdot8k-4\cdot5k}{5\cdot8k+4\cdot5k}=\dfrac{40-20}{40+20}=\dfrac{1}{3}\)

7x - 5 = 16
7x = 16 + 5
7x = 21 (Chia cả hai vế 7 để có được x)
7x/7 = 21/7
x = 3

1) \(\left(x^3-8\right):\left(x-2\right)=\left[\left(x-2\right)\left(x^2+2x+4\right)\right]:\left(x-2\right)=x^2+2x+4\)
2) \(\left(x^3-1\right):\left(x^2+x+1\right)=\left[\left(x-1\right)\left(x^2+x+1\right)\right]:\left(x^2+x+1\right)=x-1\)
3) \(\left(x^3+3x^2+3x+1\right):\left(x^2+2x+1\right)=\left(x+1\right)^3:\left(x+1\right)^2=x+1\)
4) \(\left(25x^2-4y^2\right):\left(5x-2y\right)=\left[\left(5x-2y\right)\left(5x+2y\right)\right]:\left(5x-2y\right)=5x+2y\)
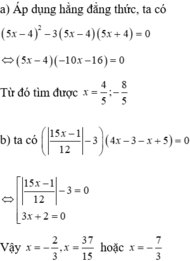
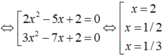
\(\left(5x-4\right)^2+3\left(16-25x^2\right)=0\)
\(\Leftrightarrow\left(5x-4\right)^2-3\left(25x^2-16\right)=0\)
\(\Leftrightarrow\left(5x-4\right)^2-3\left(5x-4\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\left(5x-4\right)\left[5x-4-3\left(5x+4\right)\right]=0\)
\(\Leftrightarrow\left(5x-4\right)\left(5x-4-15x-12\right)=0\)
\(\Leftrightarrow\left(5x-4\right)\left(-10x-16\right)=0\)
\(\Leftrightarrow5x-4=0\)hoặc \(-10x-16=0\)
\(\Leftrightarrow5x=4\) hoặc \(-2\left(5x+8\right)=0\)
\(\Leftrightarrow x=\frac{4}{5}\) hoặc \(5x+8=0\)
\(\Leftrightarrow x=\frac{4}{5}\)hoặc \(x=\frac{-8}{5}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{\frac{-8}{5};\frac{4}{5}\right\}\)
Ta có: \(\left(5x-4\right)^2-3.\left(5x-4\right).\left(5x+4\right)=0\)
\(\Leftrightarrow\left(5x-4\right).\left[\left(5x-4\right)-3\left(5x+4\right)\right]=0\)
\(\Leftrightarrow\left(5x-4\right).\left(5x-4-15x-12\right)=0\)
\(\Leftrightarrow-2.\left(5x-4\right).\left(5x+8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}5x-4=0\\5x+8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{4}{5}\\x=\frac{-8}{5}\end{cases}}\)
Vậy \(S=\left\{\frac{4}{5};\frac{-8}{5}\right\}\)