20182 -2018.2017
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
3
H
3 tháng 7 2021
a) \(153^2-53^2=\left(153-53\right)\left(153+53\right)=100.206=20600\)
b)
\(\left(2020^2-2019^2\right)+\left(2018^2-2017^2\right)+...+\left(2^2-1^2\right)\\ =\left(2020+2019\right)\left(2020-2019\right)+\left(2018+2017\right)\left(2018-2017\right)+...+\left(2+1\right)\left(2-1\right)\\ =2020+2019+2018+2017+...+2+1\\ =\dfrac{\left(2020+1\right)2020}{2}=2041210\)
AH
Akai Haruma
Giáo viên
3 tháng 7 2021
Lời giải:
a. $153^2-53^2=(153-53)(153+53)=100.206=20600$
b.
$2020^2-2019^2+2018^2-2017^2+...+2^2-1^2$
$=(2020^2-2019^2)+(2018^2-2017^2)+...+(2^2-1^2)$
$=(2020-2019)(2020+2019)+(2018-2017)(2018+2017)+...+(2-1)(2+1)$
$=2020+2019+2018+2017+...+2+1$
$=\frac{2020.2021}{2}=2041210$
LQ
2
NV
14 tháng 7 2018
\(P=\)\(-1+\frac{1}{2.1}+\frac{1}{3.2}+\frac{1}{4.3}+...+\frac{1}{2018.2017}+\frac{1}{2018}\)
\(P=-1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2017.2018}+\frac{1}{2018}\)
\(P=-1+\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2018}\)
\(P=-1+1-\frac{1}{2018}+\frac{1}{2018}\)
\(P=0\)
14 tháng 7 2018
\(P=-1+\frac{1}{2.1}+\frac{1}{3.2}+\frac{1}{4.3}+...+\frac{1}{2018.2017}+\frac{1}{2018}\)
\(P=-1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2017.2018}+\frac{1}{2018}\)
\(P=-1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2018}\)
P = 0
KH
1
11 tháng 4 2018
\(=\frac{2016.2017+2018.21+1996}{2017.2016+2018.2017}\)
\(=\frac{2018.21+1996}{2018.2017}\)
\(=\frac{21+1996}{2017}\)
\(=\frac{2017}{2017}\)
\(=1\)
J
1
29 tháng 2 2020
2018^2 + 2018.2017
= 2018.2018+2018.2017
= 2018. (2018 + 2017)
= 2018. 4035
= 8142630
26 tháng 9 2018
Mình làm bừa nha đúng đúng sai sai bạn đừng giận nhé !
\(\frac{1}{2019.2018}-\frac{1}{2018.2017}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(=\frac{1}{2019}-\frac{1}{2018}...-\frac{1}{3}-\frac{1}{2}-\frac{1}{2}-\frac{1}{1}\)
\(=\frac{1}{2019}-\left(\frac{1}{2018}-\frac{1}{2018}\right)-..-\frac{1}{1}\)
\(=\frac{1}{2019}-0-\frac{1}{1}=\frac{1}{2019}-\frac{1}{1}\)
\(=-\frac{2018}{2019}\)
26 tháng 9 2018
\(\frac{1}{2019.2018}-\frac{1}{2018.2017}-...-\frac{1}{3.2}-\frac{1}{2.1}.\)
\(=-\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{2017.2018}+\frac{1}{2018.2019}\right)\)
\(=-\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2017}-\frac{1}{2018}+\frac{1}{2018}-\frac{1}{2019}\right)\)
\(=-\left(1-\frac{1}{2019}\right)=-\frac{2018}{2019}\)
HC
4
TM
11 tháng 5 2016
x+(x+1)+(x+2)+...+(x+2016)=2018.2017
x+x+1+x+2+...+x+2016=2018.2017
(x+x+x+...+x)+(1+2+...+2016)=2018.2017
x.2017+{[(2016-1):1+1].(2016+1):2}=2018.2017
x.2017+1008.2017=2018.2017
x.2017=2018.2017-1008.2017
x.2017=2017(2018-1008)
x.2017=2017.1010
=>x=1010
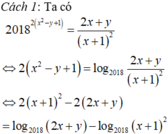
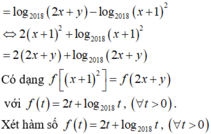
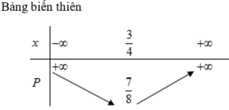
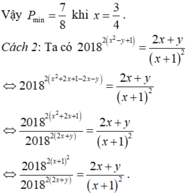
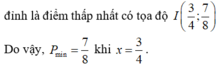
2018(2018+2017)
Trả lời:
\(2018^2+2018.2017\)
\(=2018.2018+2018.2017\)
\(=2018.\left(2017+2018\right)\)
Hok tốt!
Vuong Dong Yet