Trong mặt phẳng hệ trục tọa độ Oxy , cho tam giác ABC có A(1;-3), B(4;2), C(-2;-1) |
1) Viết phương trình tổng quát của đường thẳng A, qua A và vuông góc BC.
2) Viết phương trình tổng quát của đường thắng A, qua B và vuông góc AC.
3) Viết phương trình tổng quát của đường thẳng A, là đường trung trực của đoạn thẳng AB .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1 2022
Do C thuộc Ox nên tọa độ có dạng: \(C\left(x;0\right)\)
Do trọng tâm G thuộc Oy \(\Rightarrow x_G=0\)
Mà \(x_A+x_B+x_C=3x_G\)
\(\Rightarrow1+\left(-3\right)+x=3.0\)
\(\Rightarrow x=2\)
\(\Rightarrow C\left(2;0\right)\)
16 tháng 2 2023
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
HP
26 tháng 1 2021
Gọi G là trọng tâm tam giác ABC
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1}{3};y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{1}{3}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất khi \(3MG\) nhỏ nhất
\(\Leftrightarrow M\) là hình chiếu của \(G\) trên trục tung
\(\Leftrightarrow M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\le3MG=1\)
Đẳng thức xảy ra khi \(M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\) Tung độ \(y_M=\dfrac{1}{3}\)
CM
26 tháng 10 2019
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)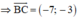 
Phương trình đường cao AH đi qua A(2;-1) nhận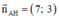 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
Lời giải:
1.
Vì ĐT cần tìm vuông góc với $BC$ nên nhận \(\overrightarrow{BC}=(-6,-3)\) là vecto pháp tuyến
PTĐT có dạng: $-6(x-1)+(-3)(y+3)=0$
$\Leftrightarrow 2x+y=-1$
2. Vì ĐT cần tìm vuông góc với $AC$ nên nhận $\overrightarrow{AC}=(-3; 2)$ là vecto pháp tuyến
PTĐT có dạng $-3(x-4)+2(y-2)=0$
$\Leftrightarrow -3x+2y=-8$
3. ĐT là trung trực của đoạn thẳng $AB$ nên:
Nhận $\overrightarrow{AB}=(3;5)$ là vecto pháp tuyến.
Đi qua trung điểm $(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2})=(\frac{5}{2};\frac{-1}{2})$
PTĐT có dạng: $3(x-\frac{5}{2})+5(y+\frac{1}{2})=0$