Có hay không số nguyên x thỏa mãn đẳng thức sau:
\(3x^5-x^3+6x^2-18x\text{=}213\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2017
Ta co:
x.(4+ x) = -3
=> x.4+x.x = -3
=> 2.x(2+1) = -3
=> 2.x.3 =-3
=> 2.x =-3:3
=>2.x =-1
=>x =-1:2
Vay x = -1:2
6 tháng 2 2018
Giả sử x,y là các số nguyên thoả mãn 9a+b=-21
Ta thấy 9a chia hết cho 3 và -21 chia hết cho 3
Khi đó b chia hết cho 3
Đặt \(b=3k\left(k\in Z\right)\)
Thay b = 3k và 9a + b = -21 ta được
\(9a+3k=-21\Rightarrow9a=-21-3k\Rightarrow a=\frac{-21-3k}{9}=\frac{-7-k}{3}\)
Vậy....
b, Làm tương tự
CM
19 tháng 12 2018
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
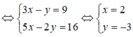
Vậy: T = |x - y| = 5
30 tháng 1 2016
|x| + |x + 1| + |x + 2| + |x + 3| = 6x (1)
a) Vì |x| >= 0; |x + 1| > 0; |x + 2| > 0; |x + 3| > 0
=> |x| + |x + 1| + |x + 2| + |x + 3| > 0
=> 6x > 0
=> x > 0
b) Vì x > 0 => |x| = x; |x + 1| = x + 1; |x + 2| = x + 2; |x + 3| = x + 3
Khi đó (1) trở thành:
x + x + 1 + x + 2 + x + 3 = 6x
=> 4x + 6 = 6x
=> 6 = 6x - 4x
=> 6 = 2x
=> x = 6/2
=> x = 3
30 tháng 1 2016
a/ vì giá trị tuyệt đối của mỗi số nguyên là số nguyên dương
suy ra IxI + Ix+1I + Ix+2I + Ix+3I là số nguyên dương
vậy x > 0 vì nếu x < 0 thì 6x là số nguyên âm
b/ ta co: x + x +1 + x + 2 + x +3 = 6x
4x + 6 = 6x nên 6 = 6x - 4x
suy ra : 6 = 2x nên x = 6 : 2 = 3
vậy x = 3
LN
3
9 tháng 10 2016
(2x + 3)2 + (3x - 2)2 = 0 mà\(\left(2x+3\right)^2\ge0;\left(3x-2\right)^2\ge0\Rightarrow\left(2x+3\right)^2+\left(3x-2\right)^2\ge0\)
\(\Rightarrow\hept{\begin{cases}\left(2x+3\right)^2=0\Rightarrow2x+3=0\Rightarrow2x=-3\Rightarrow x=-1,5\\\left(3x-2\right)^2=0\Rightarrow3x-2=0\Rightarrow3x=2\Rightarrow x=\frac{2}{3}\end{cases}}\).
Vì\(-1,5\ne\frac{2}{3}\)nên ko có x để cả 2 số hạng bằng 0,tức ko có x thỏa mãn đẳng thức đề cho
13 tháng 10 2016
Ta có : \(\left(2x+3\right)^2\ge0\)
\(\left(3x-2\right)^2\ge0\)
\(\Rightarrow\left(2x+3\right)+\left(3x-2\right)^2\ge0\)
\(\Rightarrow\begin{cases}\left(2x+3\right)^2=0\\\left(3x-2\right)^2=0\end{cases}\)
\(\Rightarrow\begin{cases}2x+3=0\\3x-2=0\end{cases}\)
\(\Rightarrow\begin{cases}2x=-3\\3x=2\end{cases}\)
\(\Rightarrow\begin{cases}x=-1,5\\x=\frac{2}{3}\end{cases}\)
Vì \(-1,5\ne\frac{2}{3}\) nên không có x để 2 số hạng bằng 0 ,có nghĩa là không có x nào thõa mãn đề bài .
Ta có: \(3x^5-x^3+6x^2-18x=213\)
\(\Rightarrow x^5-\frac{x^3}{3}+2x^2-6x=71\)
Vì x nguyên nên\(x^5,2x^2,6x\in Z\Rightarrow\frac{x^3}{3}\inℤ\)
\(\Rightarrow x^3⋮3\Rightarrow x⋮3\)(vì 3 là số nguyên tố)
Đặt x = 3k\(\Rightarrow\frac{x^3}{3}=\frac{\left(3k\right)^3}{3}=\frac{27k^3}{3}=9k^3⋮3\)
\(\Rightarrow x^5-\frac{x^3}{3}+2x^2-6x⋮3\)(vì x chia hết cho 3)
.Mà 71 chia 3 dư 2 nên không có số nguyên x thỏa mãn.
Giả sử tồn tại số nguyên x thỏa mãn đề.
Ta có : \(3x^5-x^3+6x^2-18x=213\)
Do : \(213⋮3,3x^5⋮3,6x^2⋮3,18x⋮3\)
\(\Rightarrow x^3⋮3\Rightarrow x⋮3\Rightarrow x^3⋮9\)
Lại có : \(3x^5⋮9,6x^2⋮9,18x⋮9\)
Nên : \(213⋮9\), Mặt khác \(213⋮̸9\)
Do đó không tồn tại số nguyên x thỏa mãn đề.