Bạn giúp mình tí.
-4m -1 -2m2 -2m > \(\frac{5m+5}{m-2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2021
Từ đường tròn lượng giác, trên \(\left(-\dfrac{\pi}{2};3\pi\right)\):
- Nếu \(0< t< 1\) thì \(sinx=t\) có 4 nghiệm
- Nếu \(-1< t< 0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=1\) thì \(sinx=t\) có 2 nghiệm
- Nếu \(t=-1\) thì \(sinx=t\) có 1 nghiệm
Do đó pt đã cho có 5 nghiệm pb trong khoảng đã cho khi:
\(2t^2-\left(5m+1\right)t+2m^2+2m=0\) có 2 nghiệm pb thỏa mãn:
- TH1: \(\left\{{}\begin{matrix}t_1=-1\\0< t_2< 1\end{matrix}\right.\)
- TH2: \(\left\{{}\begin{matrix}-1< 0< t_1\\t_2=1\end{matrix}\right.\)
- TH3: \(\left\{{}\begin{matrix}t_1=0\\t_2=1\end{matrix}\right.\)
Về cơ bản, chỉ cần thay 1 nghiệm bằng 0 hoặc 1 rồi kiểm tra nghiệm còn lại có thỏa hay ko là được
17 tháng 9 2021
Em làm cách khác cơ.
Δ = (...)2 nên viết hẳn 2 nghiệm ra
rồi vẽ bảng biến thiên của y = sinx
22 tháng 1 2018
Nếu m có dạng 3k thì m+3 chia hết cho 3, nếu m có dạng 3k-1 thì m-2 chia hết cho 3
28 tháng 5 2017
a, \(2mx-m^2\ge2x-2m+1\Leftrightarrow2x\left(m-1\right)\ge\left(m-1\right)^2\)
Nếu \(m-1\ge0\Leftrightarrow m\ge1\)thì
\(\Leftrightarrow2x\ge m-1\Leftrightarrow x\ge\frac{m-1}{2}\)
Nếu \(m< 1\)thì :
\(\Leftrightarrow2x\le m-1\Leftrightarrow x\le\frac{m-1}{2}\)
b,\(\Leftrightarrow2m-mx+m^2-2m+1>2x+5\Leftrightarrow m^2-4>\left(m+2\right)x\)
Nếu \(\left(m-2\right)\left(m+2\right)\ge0\Leftrightarrow\orbr{\begin{cases}m\le-2\\m\ge2\end{cases}}\)thì
\(\Leftrightarrow x< m-2\)
Nếu \(m^2-4< 0\Leftrightarrow-2< m< 2\)thì
\(\Leftrightarrow x>m-2\)
c, \(\Leftrightarrow\left(m^2-m-1-3+m\right)x>5m\)
\(\Leftrightarrow\left(m^2-4\right)x>5m\)
Nếu \(m^2-4\ge0\Leftrightarrow\orbr{\begin{cases}m\le-2\\m\ge2\end{cases}}\)thì
\(x>\frac{5m}{m^2-4}\)
Nếu \(m^2-4< 0\Leftrightarrow-2< m< 2\)thì
\(x< \frac{5m}{m^2-4}\)
CM
19 tháng 6 2018
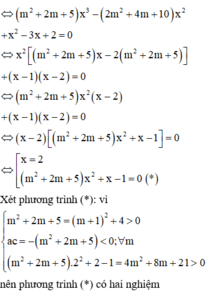
Vì f(x) là hàm đồng biến nên mỗi phương trình (1);(2);(3) đều chỉ có 1 nghiệm duy nhất và ba nghiệm của phương trình này khác nhau.
Từ đó phương trình g f x = 0 có ba nghiệm phân biệt.
Chọn: C