tính f(3) biết
f(x) = a1x1 + a2x3 + a3x5;
và f(-3) = 208
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-2\\2a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=-5\\a+b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=-2-a=-2-5=-7\end{matrix}\right.\)

Vẫn là đạo hàm của tích
Dễ dàng viết được:
\(\left[f'\left(x\right)\right]^2+f\left(x\right).f''\left(x\right)=\left[f\left(x\right)\right]'.f'\left(x\right)+f\left(x\right).\left[f'\left(x\right)\right]'=\left[f'\left(x\right).f\left(x\right)\right]'\)
Do đó giả thiết biến đổi thành:
\(\left[f'\left(x\right).f\left(x\right)\right]'=15x^4+12x\)
Nguyên hàm 2 vế:
\(f'\left(x\right).f\left(x\right)=\int\left(15x^4+12x\right)dx=3x^5+6x^2+C\)
Thay \(x=0\)
\(\Rightarrow f'\left(0\right).f\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f'\left(x\right).f\left(x\right)=3x^5+6x^2+1\)
Tiếp tục nguyên hàm 2 vế:
\(\int f\left(x\right).f'\left(x\right)dx=\int\left(3x^5+6x^2+1\right)dx\) với chú ý \(\int f\left(x\right).f'\left(x\right)dx=\int f\left(x\right).d\left[f\left(x\right)\right]=\dfrac{1}{2}f^2\left(x\right)+C\)
Nên:
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+C\)
Thay \(x=0\Rightarrow C=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+\dfrac{1}{2}\)
\(\Rightarrow f^2\left(1\right)\)

Xét khai triển 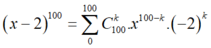 .
.
Hệ số của a97 ứng với k=3 suy ra .i k=3 suy ra ![]() .
.
Chọn A.

Lời giải:
Theo định lý Bê-du về phép chia đa thức thì để $A(x)$ chia hết cho $x+1$ thì:
$A(-1)=0$
$\Leftrightarrow -a^2+3a+6-2a=0$
$\Leftrightarrow -a^2+a+6=0$
$\Leftrightarrow a^2-a-6=0$
$\Leftrightarrow (a+2)(a-3)=0$
$\Rightarrow a=-2$ hoặc $a=3$

Ta có

Phần dư của phép chia trên là R = 6 + a – a 2 . Đề phép chia trên là phép chia hết thì R = 0 ó - a 2 + a + 6 = 0
ó - a 2 – 2a + 3a + 6 = 0
ó -a(a + 2) + 3(a + 2) = 0
ó (a + 2)(-a + 3) = 0 ó a = - 2 a = 3
Vậy có hai giá trị của a thỏa mãn điều kiện đề bài a = -2; a = 3
Đáp án cần chọn là: B

1.
y=f(-1)=3*(-1)-2=-5
y=f(0)=3*0-2=-2
y=f(-2)=3*(-2)-2=-8
y=f(3)=3*3-2=7
Câu 2,3a làm tương tự,chỉ việc thay f(x) thôi.
3b
Khi y=5 =>5=5-2*x=>2*x=0=> x=0
Khi y=3=>3=5-2*x=>2*x=2=>x=1
Khi y=-1=>-1=5-2*x=>2*x=6=>x=3
f(-1)=3.1-2=3-2=1
f(0)=3.0-2=0-2=-2
f(-2)=3.(-2)-2=-6-2=-8
f(3)=3.3-2=9-2=7
Ta có: \(f\left(-3\right)=a_1.\left(-3\right)^1+a_2.\left(-3\right)^3+a_3.\left(-3\right)^5\)
\(=-a_1.\left(3\right)^1-a_2.\left(3\right)^3-a_3.\left(3\right)^5\)
\(=-\left(a_1.\left(3\right)^1+a_2.\left(3\right)^3+a_3.\left(3\right)^5\right)\)
\(=-f\left(3\right)\)
Vì \(f\left(-3\right)=208\)
=> \(-f\left(3\right)=208\)
=> \(f\left(3\right)=-208\)