Cho a,b,c>0 tm \(a^2+b^2+c^2+abc=4\).CMR:
\(a+b+c\ge\Sigma a\sqrt{bc}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2023
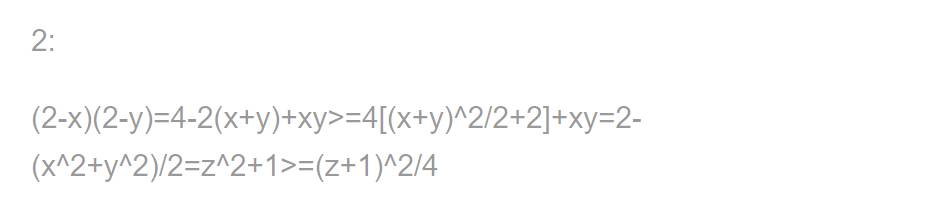
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
RD
9 tháng 12 2018
a)Bunhia:
\(\left(1+2\right)\left(b^2+2a^2\right)\ge\left(1.b+\sqrt{2}.\sqrt{2}a\right)^2=\left(b+2a\right)^2\)
b)\(ab+bc+ca=abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1\)
Áp dụng bđt câu a
=>VT\(\ge\)\(\dfrac{b+2a}{\sqrt{3}ab}+\dfrac{c+2b}{\sqrt{3}bc}+\dfrac{a+2c}{\sqrt{3}ca}\)
\(\Leftrightarrow VT\ge\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{1}{b}+\dfrac{2}{c}+\dfrac{1}{c}+\dfrac{2}{a}=3=VP\)
Tự tìm dấu "="
9 tháng 12 2018
Nguyễn Việt LâmMashiro ShiinaBNguyễn Thanh HằngonkingCẩm MịcFa CTRẦN MINH HOÀNGhâu DehQuân Tạ MinhTrương Thị Hải Anh
25 tháng 2 2018
Tuogw tựCâu hỏi của Nue nguyen - Toán lớp 10 | Học trực tuyến
Sử dụng bổ đề: \(a^2+b^2+c^2+2abc+1\ge2\left(ab+bc+ca\right)\)
Cách chứng minh bổ đề kia bằng Dirichlet google rất nhiều.
Ta có: \(2a^2+2b^2+2c^2+2abc=8\)
\(\Leftrightarrow9=a^2+b^2+c^2+\left(a^2+b^2+c^2+2abc+1\right)\ge a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow9\ge\left(a+b+c\right)^2\Rightarrow a+b+c\le3\)
\(\Rightarrow3\left(a+b+c\right)\ge\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
\(\Rightarrow a+b+c\ge ab+bc+ca=\frac{1}{2}\left[a\left(b+c\right)+b\left(c+a\right)+a\left(b+c\right)\right]\)
\(\Rightarrow a+b+c\ge\frac{1}{2}\left[a.2\sqrt{bc}+b.2\sqrt{ac}+c.2\sqrt{ab}\right]\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Tìm ra cái hướng biển đổi giả thiết này chắc lâu nhỉ ạ? Em chứng minh lúc đâu xong nó đưa ra điều cần chứng minh à \(a+b+c\le3\). Xong bí.