Cho tam giác ABC cân ở A có hai đường trung tuyến BM và CN
Chứng minh MN // BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
28 tháng 3 2023
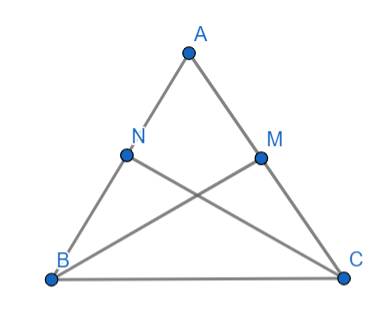
Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
27 tháng 3 2023
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN
31 tháng 10 2021
a: Xét ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)
Do đó: MN//BC
Xét tứ giác BNMC có MN//BC
nên BNMC là hình thang
mà \(\widehat{NBC}=\widehat{MCB}\)
nên BMNC là hình thang cân
2 tháng 11 2021
a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
Xét tứ giác BNMC có NM//BC
nên BNMC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BNMC là hình thang cân
8 tháng 3 2023
a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD
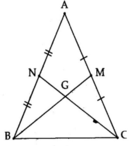
MN//BC chứ, làm gì có E -_-