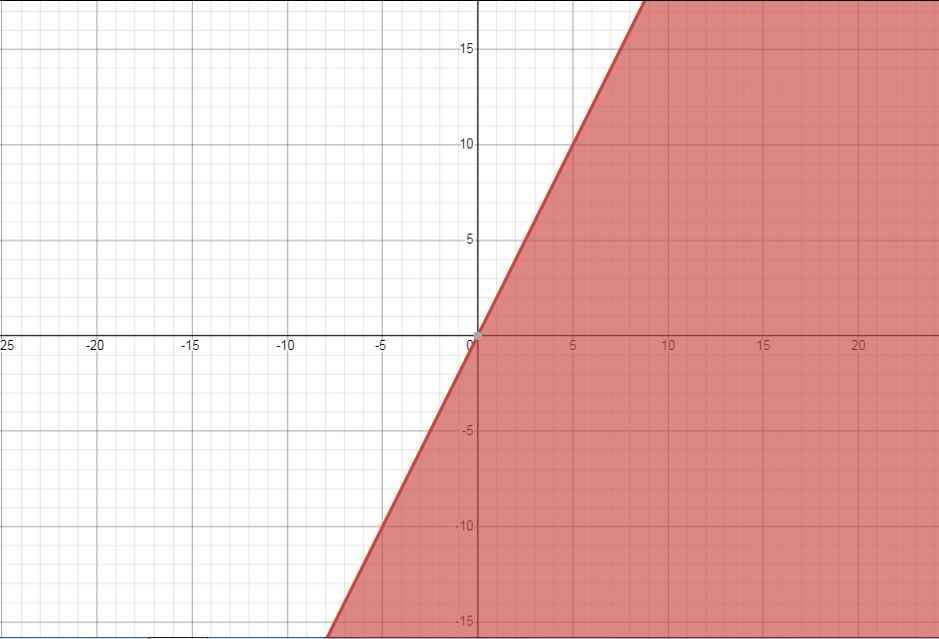
Trong các điểm tọa độ sau đây điểm nào thuộc miền nghiệm của phương trình 1/2x+3/2y>=1,x+1/2y<=2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thay tọa độ các điểm vào từng bất phương trình ta thấy, điểm (-1 ; 1) thỏa mãn cả hai bất phương trình : - 1 + 3 . 1 - 2 ≥ 0 ; 2 . - 1 + 1 + 1 ≤ 0
Do đó, điểm (-1; 1) thuộc miền nghiệm của bất phương trình đã cho.
Chọn B

Thay tọa độ các điểm vào từng bất phương trình ta thấy, điểm (-1 ; 1) thỏa mãn cả hai bất phương trình :
-1 + 3.1 - 2 ≥ 0; 2.(-1) + 1 + 1 ≤ 0
Do đó, điểm (-1; 1) thuộc miền nghiệm của bất phương trình đã cho.

Câu 1: Cặp số là nghiệm phương của 2x + 3y = 7 là:
C. ( 2;1 )
Câu 2: Phương trình x + 2y = 3, Cặp số là nghiệm phương của phương trình đã cho là cặp số : ( 1;1)

Thay tọa độ điểm (0;0) vào ta được: \(\left\{ \begin{array}{l}0 - 0 < - 3\left( {ktm} \right)\\2.0 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại A
Thay tọa độ điểm (-2;1) vào ta được: \(\left\{ \begin{array}{l} - 2 - 1 < - 3\left( {ktm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại B.
Thay tọa độ điểm (3;-1) vào ta được: \(\left\{ \begin{array}{l}3 - \left( { - 1} \right) < - 3\left( {ktm} \right)\\2.\left( { - 1} \right) \ge - 4\left( {tm} \right)\end{array} \right.\)
Loại C
Thay tọa độ điểm (-3;1) vào ta được: \(\left\{ \begin{array}{l} - 3 - 1 < - 3\left( {tm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
Chọn D.

Tham khảo:
a) Vẽ đường thẳng \(\Delta : - 2x + y - 1 = 0\) đi qua hai điểm \(A(0;1)\) và \(B\left( { - 1; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 - 1 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

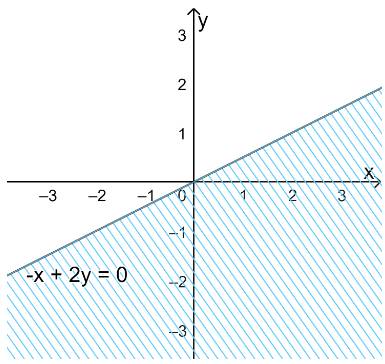
b) Vẽ đường thẳng \(\Delta : - x + 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\)
Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \( - 1 + 2.0 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), không chứa điểm A (1;0)
(miền không gạch chéo trên hình)
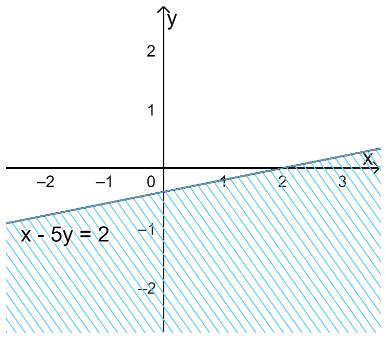
c) Vẽ đường thẳng \(\Delta :x - 5y = 2\) đi qua hai điểm \(A(2;0)\) và \(B\left( { - 3; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 5.0 = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
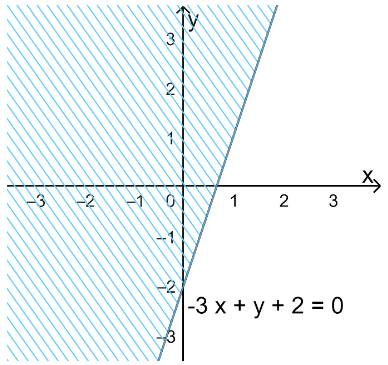
d) Vẽ đường thẳng \(\Delta : - 3x + y + 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {1;1} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 3.0 + 0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa điểm O (0;0)
(miền không gạch chéo trên hình)
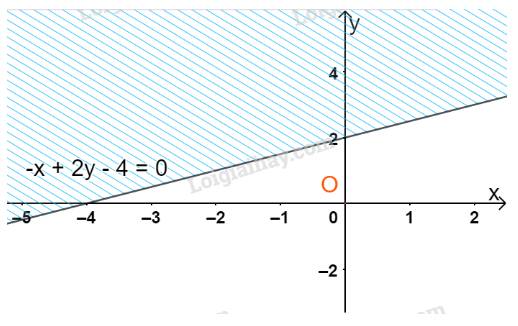
e) Ta có: \(3(x - 1) + 4(y - 2) < 5x - 3 \Leftrightarrow - 2x + 4y - 8 < 0 \Leftrightarrow - x + 2y - 4 < 0\)
Vẽ đường thẳng \(\Delta : - x + 2y -4 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {-4;0} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 2.0 -4 = -4 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa điểm O (0;0)
(miền không gạch chéo trên hình)

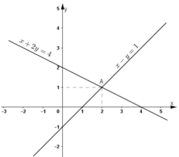
- Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
- Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.

- Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
- Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.

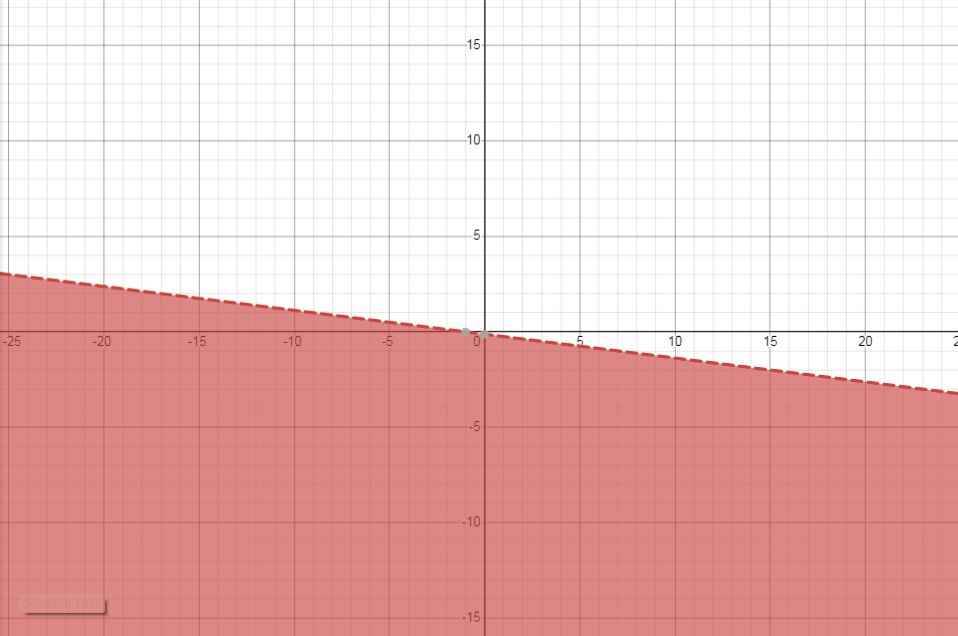
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
\(\Leftrightarrow3x-6y>4x+2y+1\)
\(\Leftrightarrow x+8y+1< 0\)
 Câu 6. Trong hình 1, biết
Câu 6. Trong hình 1, biết  Câu 7 . Trong hình 2, biết EF // BC. theo định lí Ta - lét thì tỉ lệ thức nào sau đây là đúng?
Câu 7 . Trong hình 2, biết EF // BC. theo định lí Ta - lét thì tỉ lệ thức nào sau đây là đúng?