đề bài ở dưới ạ mong các a c đừng giải theo cách vi et nhé e cảm ơn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
\(x^2+2mx+2m-6=0\)
\(\text{Δ}=\left(2m\right)^2-4\left(2m-6\right)\)
\(=4m^2-8m+24\)
\(=4m^2-8m+4+20\)
\(=\left(2m-2\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-2m}{1}=-2m\\x_1x_2=\dfrac{c}{a}=\dfrac{2m-6}{1}=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2=20\)
=>\(\left(-2m\right)^2-4\left(2m-6\right)=20\)
=>\(4m^2-8m+24-20=0\)
=>\(4m^2-8m+4=0\)
=>\(\left(2m-2\right)^2=0\)
=>2m-2=0
=>2m=2
=>m=1(nhận)
Câu 4:
a: \(2x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot2\cdot\left(-m\right)\)
\(=4+8m\)
Để phương trình có hai nghiệm phân biệt thì 8m+4>0
=>8m>-4
=>\(m>-\dfrac{1}{2}\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{2}=\dfrac{2}{2}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\cdot\left(x_1^2+x_2^2\right)=16\)
=>\(\left(1+\dfrac{m}{2}\right)^2+4\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=16\)
=>\(\left(\dfrac{m+2}{2}\right)^2+4\left[1^2-2\cdot\dfrac{-m}{2}\right]=16\)
=>\(\dfrac{1}{4}\left(m^2+4m+4\right)+4\left(1+m\right)=16\)
=>\(\dfrac{1}{4}m^2+m+1+4+4m-16=0\)
=>\(\dfrac{1}{4}m^2+5m-11=0\)
=>\(m^2+20m-44=0\)
=>(m+22)(m-2)=0
=>\(\left[{}\begin{matrix}m+22=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-22\left(loại\right)\\m=2\left(nhận\right)\end{matrix}\right.\)
5.
\(\Delta'=1+2m\)
a.
Phương trình có 2 nghiệm pb khi:
\(1+2m>0\Rightarrow m>-\dfrac{1}{2}\)
b.
Khi pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\left(x_1^2+x_2^2\right)=16\)
\(\Leftrightarrow\left(1-x_1x_2\right)^2+4\left(x_1+x_2\right)^2-8x_1x_2=16\)
\(\Leftrightarrow\left(1+\dfrac{m}{2}\right)^2+4.1^2+4m=16\)
\(\Leftrightarrow\dfrac{m^2}{4}+5m-11=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-22< -\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
5.
\(\Delta'=m^2-\left(2m-6\right)=\left(m-1\right)^2+5>0;\forall m\)
Pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+20\)
\(\Leftrightarrow4m^2=4\left(2m-6\right)+20\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

Bây giờ tôi và Linh đã là những học sinh giỏi toàn diện, là những đội viên gương mẫu của trường, đặc biệt chúng tôi luôn là những chủ công xuất sắc trong những cuộc thi học sinh giỏi của huyện và tỉnh. Thời gian trôi qua nhanh thật! Nghĩ lại, tôi mới thấy tình bạn thật là kỳ diệu.
Trong lớp 4A hồi ấy, tôi được bạn bè khẳng định là một thằng thông minh nhưng lỳ lợm. Tôi và Linh không ghét nhau nhưng những lời gán ghép trêu chọc của bạn bè khiến chúng tôi chẳng bao giờ nói chuyện. Ở trong lớp, ngoài Hùng thì Linh là đứa học ngang ngửa với tôi. Tất cả sẽ chẳng có gì thay đổi nếu như không có một ngày.
Hôm ấy, giữa buổi học thằng Hùng ốm xin phép cô về trước. Nó nhờ tôi mang chiếc cặp về sau. Buổi học tan, trời bông dưng đổ mưa tầm tã. Tôi nán lại chút ít hỏi cô về một bài toán khó. Hỏi xong, bước ra khỏi lớp tôi chỉ thấy lác đác còn một vài bạn ở sân trường. Mưa vẫn như trút nước làm những lá bằng lăng ướt sũng, trĩu xuống quệt ngang đầu. Đám cỏ trong bồn hoa "mênh mông trong bể nước". Tôi mặc áo mưa cẩn thận, che kín hai chiếc cặp rồi vội vã bước đến nhà xe. Nhưng lạ thật! Tôi chưa phải là người về cuối cùng trong lớp, vẫn còn một chiếc xe của ai đó. Hình như nó giống xe của Ngọc Linh. Nhìn quanh, tôi thấy Linh vẫn đứng ngay ở cột salon trước cửa lớp, chỗ tôi vừa đi qua nhưng không để ý. Tôi đoán Linh không có áo mưa.
Kệ! Mình cứ về không mai lại nghe tụi nó ca "bài ca bất tử”, tôi nghĩ. Và tôi quyết định phóng xe. Nhưng vừa ra tới cổng, tôi nhớ ra mình còn dư một chiếc áo mưa trong cặp của Hùng. Giá như không có mình về cùng chẳng sao, nhưng,…
– Áo mưa này Linh, cậu về đi không tối, tôi đứng trước mặt Linh.
Hôm đó, đi đến giữa đường, tôi gặp bố Linh đi đón bạn. Bố Linh đã mời tôi về nhà và cảm ơn tôi.
Sáng hôm sau, không hiểu sao bọn lớp tôi lại biết và đúng như tôi dự đoán, bọn nó lại ca những bài ca cũ. Nhưng khác hẳn với mọi hôm, hôm nay, Linh bước đến bàn tôi nói:
– Cảm ơn cậu, từ nay bọn mình sẽ là bạn của nhau nhé!
Từ đó, thỉnh thoảng tôi và Linh lại trao đổi với nhau về những bài toán hay bài văn khó. Lũ bạn thấy tụi tôi chơi thân, cũng không còn trêu chọc nữa. Thế là tôi và Linh trở thành bạn tốt.
Năm vừa qua, tôi và Linh rất mừng khi được huyện chọn đi thi học sinh giỏi tỉnh và cả hai đều đoạt giải. Lên cấp hai, chúng tôi hứa với cô giáo cũ sẽ lại cùng giúp nhau để học tập tốt hơn.
Thế đấy các bạn ạ! Từ một việc làm rất nhỏ thôi, tôi đã có được một tình bạn lớn. Bây giờ thì tôi đã hiểu sâu sắc câu ngạn ngữ: Tình bạn là thứ quý giá nhất trên đời.

Bài làm
"Tùng,tùng"mỗi khi nghe tới tiếng trống đó em lại không thể nào quên được những ngày vui nhộn của thời học sinh,nó đã gắn bó với em trong suốt 5 năm học tiểu học.Dù sau này có đi đâu thì em vẫn luôn nhớ về cái trống trường-người bạn thời ấu thơ.
K CHO MK NHA,NẾU KO HAY THÌ THUI

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)
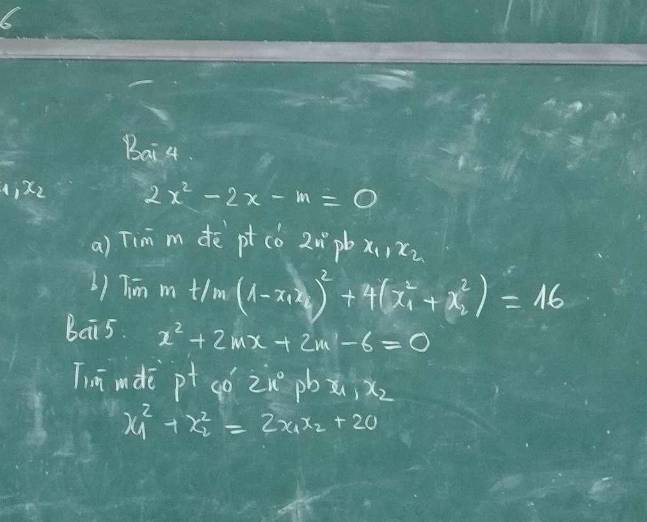
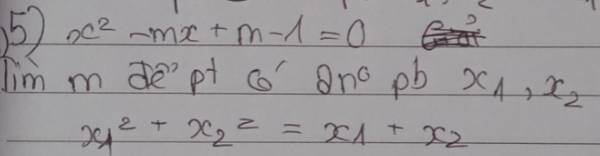
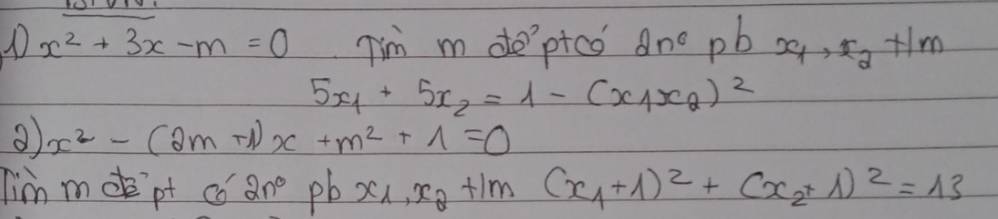


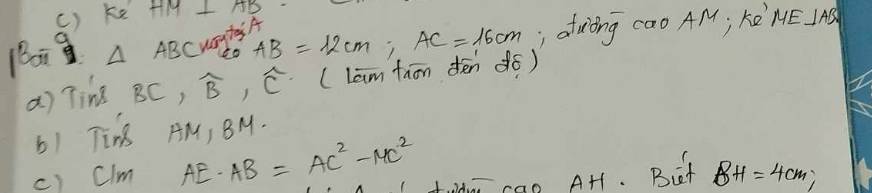
a) ta có : \(\Delta'=\left(m-3\right)^2\ge0\forall m\)
==> phương trình lun có nghiệm với mọi m (đpcm)
b) \(x_1=\frac{-b'+\sqrt{\Delta}}{a}=m-2+\sqrt{\left(m-3\right)^2}=2m-5\)
\(x_1=\frac{-b'-\sqrt{\Delta}}{a}=m-2-\sqrt{\left(m-3\right)^2}=1\)
ta có : \(x_1\left(1-x_2\right)+x_2\left(1-x_1\right)< 4\Leftrightarrow x_1+x_2-2x_1x_2-4< 0\)
\(\Leftrightarrow2m-5+1-2\left(2m-5\right)-4< 0\Leftrightarrow m>1\)
vậy ......