cho hình thoi abcd có canh ab dài 10cm;ac=12cm kẻ ah vuông góc bc.
a,tính diện tích hình thoi
b,tính ah
b,gọi i là trung điểm cd,e là điểm đối xứng a qua i. chứng minh rằng bd vuông góc de và tính diện tích tam giác bde
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
7 tháng 8 2023
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
26 tháng 3 2020
Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
CM
2 tháng 3 2018
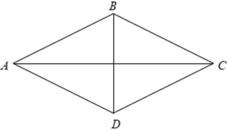
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HA = HC = 5( cm )
Áp dụng định lí Py – to – go ta có:
NT
1
7 tháng 10 2019
A B C D I
Vì : ABCD là hình thoi
\(\Rightarrow IA=IC=\frac{AC}{2}=\frac{12}{2}=6\)
Xét \(\Delta ABI\) vuông tại I
\(\Rightarrow AB^2=AI^2+BI^2\)
\(\Rightarrow BI^2=AB^2-AI^2=10^2-6^2=64\)
\(\Rightarrow BI=8\)
\(\Rightarrow BD=2.BI=2.8=16\)
Diện tích hình thoi ABCD là :
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\)
Chúc bạn học tốt !!!
5 tháng 9 2023
Lời giải
a) Tính diện tích hình thang BHDA
Do E là điểm chính giữa cạnh AB nên EA = AB/2 = 5cm.
Do H là điểm chính giữa cạnh BC nên BH = BC/2 = 5cm.
Do đó, đáy lớn của hình thang BHDA là BH + AD = 5 + 10 = 15cm.
Do hình thang BHDA là hình thang cân có đáy lớn bằng đáy bé nên diện tích của hình thang BHDA là:
S = 1/2 * (15 + 15) * 10 = 112.5cm^2b) Tính diện tích tam giác AHE và diện tích tam giác AHD
Do E là điểm chính giữa cạnh AB nên AE = AB/2 = 5cm.
Do H là điểm chính giữa cạnh BC nên BH = BC/2 = 5cm.
Do đó, diện tích tam giác AHE là:
S = 1/2 * AE * BH = 1/2 * 5 * 5 = 12.5cm^2Tương tự, diện tích tam giác AHD là 12.5cm^2.
Kết luận
- Diện tích hình thang BHDA = 112.5cm^2
- Diện tích tam giác AHE = Diện tích tam giác AHD = 12.5cm^2