TÌM a, b SAO CHO \(a-b=4\)VÀ \(\overline{87ab}\)\(⋮9\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
2
18 tháng 5 2017
Để : \(\overline{87ab}⋮9\Rightarrow\left(8+7+a+b\right)⋮9\)
\(\Rightarrow\left(15+a+b\right)⋮9\Rightarrow9+\left(6+a+b\right)⋮9\)
Vì \(9⋮9\Rightarrow6+a+b⋮9\)
\(\Rightarrow a+b=3\) hoặc \(a+b=12\)
Mà : a - b = 4
+) \(\Rightarrow\left\{{}\begin{matrix}a+b=3\\a-b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a\in\varnothing\\b\in\varnothing\end{matrix}\right.\)
+) \(\Rightarrow\left\{{}\begin{matrix}a+b=12\\a-b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=8\\b=4\end{matrix}\right.\)
Vậy a = 8 ; b = 4 thỏa mãn đề bài
3 tháng 10 2017
Để \(\overline{87ab}\)\(⋮\) 9 thì ( 8 + 7 + a + b ) sẽ chia hết cho 9
( 8 + 7 + a + b ) = ( 15 + a + b ) = 9 + ( 6 + a + b )
Mà 9 chia hết cho 9 nên ta còn 6 + a + b chia hết cho 9
Để 6 + a + b chia hết cho 9 thì tổng a + b = 3 hoặc 12 ( không thể có số lớn hơn vì 2 số lớn nhất có 1 cs cũng chỉ có tổng là 18 mà 12+9 = 21 , 21>18 nên a+ b = 3 hoặc 12 )
Mà a - b = 4 nên ta có các trường hợp sau :
_Nếu a+ b = 3 thì không thể có a - b = 4 Trường hợp sai
_Nếu a + b = 12 thì :
+) a= 4 hoặc 5 hoặc 6 hoặc 7 hoặc 8 hoặc 9 hoặc ... hoặc 12
+) b= 0 hoặc 1 hoặc 2 hoặc 3 hoặc ... hoặc 8
Mà ta thấy a = 8 , b = 4 là thỏa mãn đầu bài nên a = 8 , b = 4 .
PT
1
CM
6 tháng 1 2019
Ta có: 87ab ⋮ 9 ⇔ (8 + 7 + a + b) ⁝⋮ 9 ⇔ (15 + a + b) ⋮ 9
Suy ra: (a + b) ∈ {3; 12}
Vì a – b = 4 nên a + b > 3. Suy ra a + b = 12
Thay a = 4 + b vào a + b = 12, ta có:
b + (4 + b) = 12 ⇔ 2b = 12 – 4
⇔ 2b = 8 ⇔ b = 4
a = 4 + b = 4 + 4 = 8
Vậy ta có số: 8784.
PT
1
CM
18 tháng 9 2018
b) Ta có: 0 <a < b ≤ 18 nên 15 < 8+7+a+b ≤ 33
mà (8+7+a+b) ⋮ 9
Nên a+b=3 hoặc a+b=12 mặt khác a = b + 4 nên a - b = 4
suy ra a = 3,5 và b = -0,5 (loại) hoặc a = 8; b = 4 (thỏa mãn)
Vậy a=8; b=4
PT
1
CM
10 tháng 6 2019
b) Ta có 0 < a + b ≤ 18 nên 15 ≤ 8 + 7 + a + b ≤ 33 mà (8 + 7 + a + b) ⋮ 9
a + b = 3 hoặc a + b = 12 mặt khác a = b + 4 a – b = 4
a = 3, 5 và b = -0,5(loại) hoặc a = 8; b = 4 (thỏa mãn)
Vậy a = 8; b = 4.
PT
1
PT
1
CM
15 tháng 5 2018
Ta có 0 < a + b ≤ 18 nên 15 ≤ 8 + 7 + a + b ≤ 33 mà (8 + 7 + a + b) ⋮ 9
a + b = 3 hoặc a + b = 12 mặt khác a = b + 4 a – b = 4
a = 3, 5 và b = -0,5(loại) hoặc a = 8; b = 4 (thỏa mãn)
Vậy a = 8; b = 4.
PT
1
CM
20 tháng 10 2017
Sơ đồ con đường |
Lời giải chi tiết |
|
Vì a − b = 4 ⇒ a = b + 4 . Mà 87 a b ¯ ⋮ 9 ⇒ 15 + a + b ⋮ 9 ⇒ 19 + 2 b ⋮ 9 ⇒ b = 4 ; a = 8 |
TC
3
TC
6 tháng 1 2022
87ab chia hết cho 9 nên tổng 8 + 7 + a+ b = 15 + a+ b chia hết cho 9
a + b < 10 + 10 = 20 nên a + b có thể bằng 3; 12;
+) Nếu a + b = 3 ; có a - b = 4 => a = (3+4):2 = 3,5 Loại vid a là chữ số
+) Nếu a + b = 12 , có a - b = 4 => a = (12 + 4): 2 = 8 => b = 12 - 8 = 4
Vậy a = 8; b = 4
6 tháng 1 2022
87ab chia hết cho 9 => 8 + 7 + a + b chia hết cho 9
=> 15 + a + b chia hết cho 9
=>a ,b thuộc { 3; 12}
Ta có : a - b = 4
=> a +b = 3 (loại)
Từ a - b = 4 và a + b = 12, suy ra
a = 8 ; b = 4
tick nha
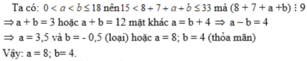
Để \(\overline{87ab}⋮9\)thì \(8+7+a+b⋮9\)
\(\Leftrightarrow15+a+b⋮9\)
mà a, b là các chữ số \(\Rightarrow0\le a+b\le18\)\(\Rightarrow a+b\in\left\{3;12\right\}\)
Vì a, b là các chữ số \(\Rightarrow a+b\ge a-b\)\(\Rightarrow\)\(a+b=12\)thoả mãn
mà \(a-b=4\)\(\Rightarrow\left(a+b\right)+\left(a-b\right)=12+4\)
\(\Leftrightarrow2a=16\)\(\Leftrightarrow a=8\)\(\Rightarrow a=8-4=4\)
Vậy \(a=8\)và \(b=4\)
Do a, b là các chữ số nên a, b thuộc N, \(0\le a\le9;0\le b\le9\Rightarrow0\le a+b\le18\)(1)
87ab chia hết cho 9 nên 8+7+a+b chia hết cho 9 => 15+a+b chia hết cho 9 => 9+6+a+b chia hết cho 9 => 6+a+b chia hết cho 9(2)
Từ (1) và (2) => \(\left(a+b\right)\in\left\{3;12\right\}\)(3)
a-b=4 (4)
Từ (3) và (4) ta xét hai trường hợp:
Trường hợp 1:\(\hept{\begin{cases}a+b=3\\a-b=4\end{cases}\Leftrightarrow2a=7\Leftrightarrow a=\frac{7}{2}}\)(loại vì a thuộc N)
Trường hợp 2: \(\hept{\begin{cases}a+b=12\\a-b=4\end{cases}\Leftrightarrow2a=16\Leftrightarrow a=8\Rightarrow b=4}\)
vậy \(\left(a,b\right)\in\left\{\left(8,4\right);\left(4,8\right)\right\}\)