cho hàm số y=(m+1)x+3. tìm m để khoảng cách từ gốc tọa độ đến đồ thị hàm số có giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2019
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
CM
9 tháng 8 2017
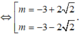
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
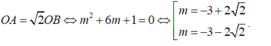
Tổng hai giá trị này là -6.
Chọn C.
25 tháng 10 2021
a: Thay x=1 và y=2 vào (d), ta được:
2m+1=2
hay \(m=\dfrac{1}{2}\)
25 tháng 10 2021
Thay x=1 và y=2 vào (d), ta được:
2m+1=2
hay \(m=\dfrac{1}{2}\)
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Đặt: d: y = ( m+1 ) x + 3
+) TH1: m = -1
=> d: y = 3
=> Khoảng cách của gốc tọa độ tới d là: 3 (1)
+) Th2: m khác -1.
Giao điểm của d với Ox là : A ( \(-\frac{3}{m+1};0\))
=> \(OA=\left|\frac{3}{m+1}\right|\)
Giao điểm của d với Oy là: \(B\left(0;3\right)\)
=> OB = 3.
Kẻ OH vuông với d tại H => AH là khoảng cách từ O tới d
Xét tam giác OAB vuông tại O. Có OH là đường cao:
=> \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{\left(m+1\right)^2}{9}+\frac{1}{9}>\frac{1}{9}\)vì m khác 1 => \(\left(m+1\right)^2>0\)
=> \(OH< 3\)
=> Khoảng cách từ gốc tọa độ đến d nhỏ hơn 3 (2)
Từ (1); (2) Khoảng cách từ O đến d có giá trị lớn nhất là 3 đạt tại m = -1.
len google bn oi