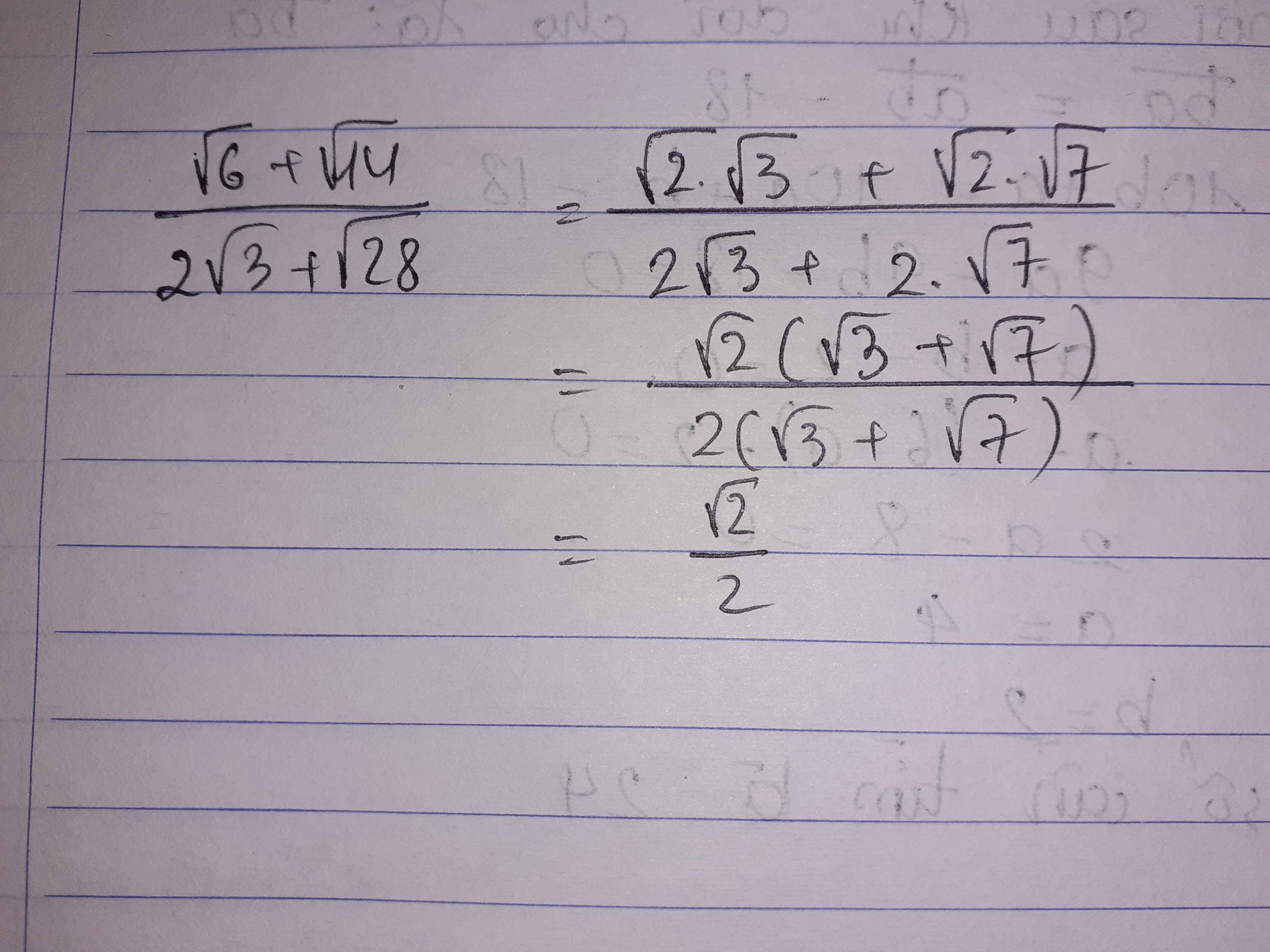Rút gọn biểu thức sau:
\(\sqrt{62-20\sqrt{6}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
V
0
Những câu hỏi liên quan
2
24 tháng 9 2023
`a)(\sqrt{14}-3\sqrt{2})^2+6\sqrt{28}`
`=14-12\sqrt{7}+18+12\sqrt{7}=32`
`b)2\sqrt{20}-3\sqrt{20}+\sqrt{125}`
`=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}`
`=3\sqrt{5}`.
H9
HT.Phong (9A5)
CTVHS
24 tháng 9 2023
a) \(\left(\sqrt{14}-3\sqrt{2}\right)^2-6\sqrt{28}\)
\(=\left(\sqrt{14}\right)^2-2\cdot\sqrt{14}\cdot3\sqrt{2}+\left(3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-6\sqrt{28}+18+6\sqrt{28}\)
\(=14+18\)
\(=32\)
b) \(2\sqrt{20}-3\sqrt{20}+\sqrt{125}\)
\(=2\cdot2\sqrt{5}-3\cdot2\sqrt{5}+5\sqrt{5}\)
\(=4\sqrt{5}-6\sqrt{5}+5\sqrt{5}\)
\(=3\sqrt{5}\)
18 tháng 9 2021
\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\left|2+\sqrt{2}\right|-\left|2-\sqrt{2}\right|\)
\(=2+\sqrt{2}-2+\sqrt{2}=2\sqrt{2}\)
VT
2
7 tháng 12 2016
\(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
\(=\sqrt{4.5}-\sqrt{9.5}+3\sqrt{18}+\sqrt{4.18}\)
\(=2\sqrt{5}-3\sqrt{5}+3\sqrt{18}+2\sqrt{18}\)
\(=-\sqrt{5}+5\sqrt{18}\)
TK
1
21 tháng 12 2023
Sửa đề: \(\sqrt{11-6\sqrt{2}}+\sqrt{3-2\sqrt{2}}\)
\(=\sqrt{9-2\cdot3\cdot\sqrt{2}+2}+\sqrt{2-2\cdot\sqrt{2}\cdot1+1}\)
\(=\sqrt{\left(3-\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\left|3-\sqrt{2}\right|+\left|\sqrt{2}-1\right|\)
\(=3-\sqrt{2}+\sqrt{2}-1\)
=3-1=2
MN
0
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 1 2022
Đặt \(x=\sqrt{\dfrac{5+2\sqrt{6}}{5-\sqrt{6}}}+\sqrt{\dfrac{5-2\sqrt{6}}{5+\sqrt{6}}}>0\)
\(x^2=\dfrac{5+2\sqrt{6}}{5-\sqrt{6}}+\dfrac{5-2\sqrt{6}}{5+\sqrt{6}}+2\sqrt{\dfrac{25-24}{25-6}}=\dfrac{74}{19}+\dfrac{2\sqrt{19}}{19}\)
\(\Rightarrow x^2=\dfrac{74+2\sqrt{19}}{19}\Rightarrow x=\sqrt{\dfrac{74+2\sqrt{19}}{19}}\)
Ko thể rút gọn thêm nữa (có thể trục căn thức ở mẫu)
N
2
3 tháng 2 2020
\(A=\sqrt{8+\sqrt{8}+\sqrt{20}+\sqrt{40}}\)
\(=\sqrt{\sqrt{5}^5+\sqrt{2}^2+1^2+2\sqrt{2}.1+2\sqrt{2}.\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}+\sqrt{2}+1\right)^2}\)
\(=\sqrt{5}+\sqrt{2}+1\)
16 tháng 9 2021
\(A=\sqrt{5-2\sqrt{6}}-\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}\)
=0