Tìm tất cả giá trị thực của tham số m để hàm số y=x^3-3mx^2-9m^2x nghịch biến trên khoảng (0;1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
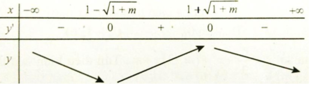
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.

Đáp án B
Ta có y ' = m x 2 − 2 m + 1 x + m − 2. Hàm số nghịch biến trên − ∞ ; + ∞ ⇔ y ' ≤ 0 , ∀ x ∈ − ∞ ; + ∞ .
TH1: m = 0 ⇒ y ' ≤ 0 ⇔ − 2 x − 2 ≤ 0 ⇔ x ≥ − 1 ⇒ hàm số không nghịch biến trên − ∞ ; + ∞
TH2: m ≠ 0 ⇒ y ' ≤ 0 , ∀ x ∈ − ∞ ; + ∞ ⇔ m < 0 Δ ' y ' ≤ 0 ⇔ m < 0 m + 1 2 − 3 m m − 2 ≤ 0 ⇔ m < 0 m ≤ − 1 4 ⇒ m ≤ − 1 4 Kết hợp 2 TH, suy ra m ≤ − 1 4 .

Đáp án A
Có y ' = m 2 − m − 2 x + m 2 . Hàm số nghịch biến trên − 1 ; + ∞ ⇔ m 2 − m − 2 < 0 ⇔ m ∈ − 2 ; 1

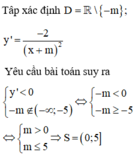
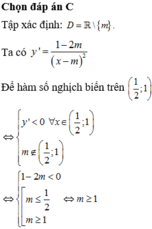

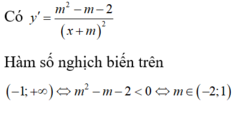
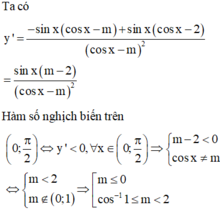
\(y'=3x^2-6mx-9m^2,y'=0\Leftrightarrow\left[{}\begin{matrix}x=-m\\x=3m\end{matrix}\right.\)
Với m=0 thỏa mãn
Dựa vào bảng biến thiên suy ra \(m\ge\frac{1}{3}\) hoặc \(m\le-1\)
Cách khác:
Bạn dùng tính chất sau:Cho hàm số \(f\left(x\right)=ax^2+bx+c\) có 2 nghiệm \(x_1< x_2\) thì \(x_1\le\alpha< \beta\le x_2\Leftrightarrow\left\{{}\begin{matrix}af\left(\alpha\right)\le0\\af\left(\beta\right)\le0\end{matrix}\right.\)
Hàm số nghịch biến trên khoảng (0,1) tương đương với \(y'\le0\) với mọi x thuộc (0,1)
Với m=0 thỏa mãn, xét m khác 0
\(\Delta'_{y'}=36m^2>0\forall m\ne0\) nên y' luôn có hai nghiệm phân biệt \(x_1,x_2\)
\(y'\le0\forall x\in\left(0;1\right)\Leftrightarrow x_1\le0< 1\le x_2\\ \Leftrightarrow\left\{{}\begin{matrix}3y'\left(0\right)\le0\\3y'\left(1\right)\le0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\ge\frac{1}{3}\\m\le-1\end{matrix}\right.\)