Tìm m để pt: x2 -2(m+1)x + 2m +10=0 có 2 nghiệm pb x1, x2 thỏa x12 + x22=64 -10x1x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 11 2021
Để PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m-1\right)^2-4\left(m+6\right)\ge0\)
\(\Leftrightarrow m^2-6m-23\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\le3-4\sqrt{2}\\m\ge3+4\sqrt{2}\end{matrix}\right.\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=1-m\\x_1x_2=m+6\end{matrix}\right.\)
\(x_1^2+x_2^2=10\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\\ \Leftrightarrow\left(1-m\right)^2-2\left(m+6\right)=10\\ \Leftrightarrow m^2-2m+1-2m-12=10\\ \Leftrightarrow m^2-4m-21=0\\ \Leftrightarrow\left[{}\begin{matrix}m=7\left(ktm\right)\\m=-3\left(tm\right)\end{matrix}\right.\Leftrightarrow m=-3\)
VD
11 tháng 3 2022
Bài 1:
a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\
\Leftrightarrow x^2+1+7=0\\
\Leftrightarrow x^2+8=0\left(vô.lí\right)\)
Thay m=3 vào (1) ta có:
\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
b, Thay x=4 vào (1) ta có:
\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)
c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)
VD
11 tháng 3 2022
Bài 2:
a,Thay m=-2 vào (1) ta có:
\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)
\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)
\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)
\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)
CM
31 tháng 12 2017
Phương trình x 2 – 2mx + 2m − 1 = 0 có a = 1 ≠ 0 và = 4 m 2 – 4 (2m – 1)
= 4 m 2 – 8 m + 4 = 4 ( m – 1 ) 2 ≥ 0 ; ∀ m
Phương trình có hai nghiệm x 1 ; x 2 với mọi m
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m x 1 . x 2 = 2 m − 1
Xét
x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 ⇔ 4 m 2 – 2 ( 2 m – 1 ) = 10
⇔ 4 m 2 – 4 m + 2 – 10 = 0 ⇔ 4 m 2 – 4 m – 8 = 0 ⇔ m 2 – m – 2 = 0
m 2 – 2 m + m – 2 = 0 ⇔ m ( m – 2 ) + ( m – 2 ) = 0 ⇔ ( m + 1 ) ( m – 2 ) = 0
⇔ m = 2 m = − 1
Vậy m = 2 và m = −1 là các giá trị cần tìm
Đáp án: D
AH
Akai Haruma
Giáo viên
26 tháng 5 2022
Bạn có thể tham khảo bài này. Hướng giải tương tự.
https://hoc24.vn/cau-hoi/cho-phuong-trinh-x2-4xm0m-la-tham-soa-tinh-cac-gia-tri-cua-m-de-phuong-trinh-co-cac-nghiem-x1x2-thoa-man-x1-x2-va-x22-x1218.6292592319064
24 tháng 3 2023
Δ=(m+1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24
=>Phương trình luôn có hai nghiệm pb
x1^2+x2^2+(x1-2)(x2-2)=11
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2-7=0
=>m^2-2m-8=0
=>(m-4)(m+2)=0
=>m=4 hoặc m=-2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2021
Giả sử pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-n\\x_1x_2=2m+3n-1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1^2+x_2^2=13\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-1\\\left(x_1+x_2\right)^2-2x_1x_2=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-n=-1\\2m+3n-1=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=-1\\m=-1\end{matrix}\right.\)
TA
27 tháng 5 2021
PT có 2 nghiệm phân biệt`<=> \Delta' >0`
`<=> m^2-1>0`
`<=> m<-1 ; 1 <m`
Viet: `x_1+x_2=2m`
`x_1x_2=1`
Theo đề: `x_1^2+x_2^2=8`
`<=> (x_1+x_2)^2-2x_1x_2=8`
`<=> 4m^2-2=8`
`<=> 4m^2 - 10=0`
`<=>` \(\left[{}\begin{matrix}m=\dfrac{\sqrt{10}}{2}\\m=-\dfrac{\sqrt{10}}{2}\end{matrix}\right.\)
Vậy `m=\pm \sqrt10/2`.
12 tháng 3 2022
a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1
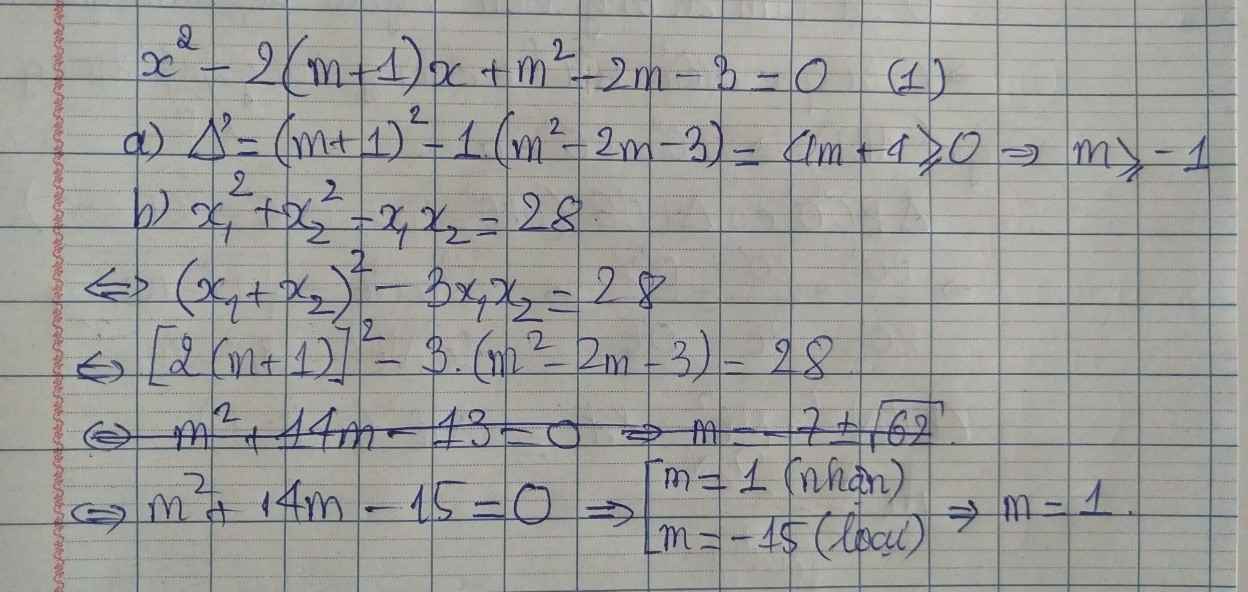
\(\Delta'=\left(m+1\right)^2-2m-10=m^2-9\)
để pt có 2 no pb => \(\Delta'\ge0\Rightarrow m^2-9\ge0\Rightarrow\left\{{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
pt trên có no thì:
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=2m+1\end{matrix}\right.\)
mà
\(x_1^2+x_2^2+10x_1x_2=64\\ \Leftrightarrow\left(x_1+x_2\right)^2+6x_1x_2=64\\ \Leftrightarrow\left(2m+2\right)^2+6\left(2m+1\right)=64\\ \Leftrightarrow4m^2+20m+10-64=0\\ \Leftrightarrow.....\)
vậy m=...