Hộ em phần c bài này ạ
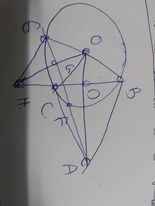
Cho đường tròn (O;R) đường kính AB và điểm P ở ngoài đường tròn. Từ P kẻ các tiếp tuyến PA và PM tới đường tròn ( A và M là các tiếp điểm ).
a)Chứng minh 4 điểm A,P,M,O cùng thuộc 1 đường tròn.
b)Gọi C là giao điểm của đường tròn (O) và PB. chứng minh BC.BP = 4R2
c)Kẻ MH vuông góc AB cắt PB tại I. Chứng minh I là trung điểm của MH